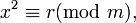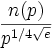En Matemáticas, dentro de la Teoría de Números se denomina residuo cuadrático módulo m a cualquier entero r primo con m para el que tenga solución la congruencia:

o lo que es lo mismo cuando r es un cuadrado perfecto módulo m, y que por lo tanto tiene una raíz cuadrada en la aritmética de módulo m. A los enteros que no son congruentes con cuadrados perfectos módulo m se les denomina no-residuos cuadráticos. En adelante nos referimos a menudo a ellos como residuos y no-residuos.

Por ejemplo cuando el módulo es 13, los residuos son: 1, 3, 4, 9, 10 y 12, y los no residuos 2, 5, 6, 7, 8, y 11. En general para determinar cuales son los residuos cuadráticos para un módulo dado, basta con determinar los restos de dividir por m a los cuadrados perfectos de los enteros primos con m y menores o iguales a m / 2.

En el estudio de los residuos cuadráticos es conveniente limitarse al caso en el que el módulo es un primo p, ya que entonces tenemos un comportamiento mucho más sencillo, y muchas propiedades de los residuos para módulos generales pueden derivarse de este caso usando el teorema chino del resto, y otros resultados de la resolución de congruencias. Para estudiar este caso es muy conveniente el uso del símbolo de Legendre, y de su extensión el símbolo de Jacobi.

Propiedades

Los residuos cuadráticos tienen varias propiedades muy sencillas de demostrar, por ejemplo el producto de dos residuos o de dos no--residuos es un residuo y el producto de un residuo y de un no-residuo es un no-residuo. Por ejemplo en las listas del ejemplo anterior siempre que multipliquemos dos elementos de la misma lista obtenemos un número en la primera lista 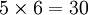que es congruente con 4, que es un elemento de la primera lista. Mientras que si multiplicamos un elemento de la primera lista por uno de la segunda obtenemos siempre un elemento de la segunda lista 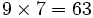que es congruente con 11 que está en la segunda lista).

i) La mitad de las p − 1 clases residuales módulo p son residuos y la otra mitad no-residuos. En el ejemplo anterior la mitad se encuentran en la primera lista y la otra mitad en la segunda, de acuerdo con la propiedad enunciada.

ii) -1 es un residuo de todos los primos de la sucesión 4k + 1 y es un no-residuo de todos los primos de la sucesión 4k + 3

iii) 2 es un residuo de todos los primos de las sucesiones 8k + 1 y 8k + 7 y es un no-residuo de todos los demás primos impares.

iv) Si p y q son primos impares, y ninguno de ellos pertenece a la sucesión 4k + 1 entonces p es un residuo módulo q si y sólo si q es un no-residuo módulo p. Si por otro lado cualquiera de los dos, o ambos, pertenecen a la sucesión 4k + 1 entonces p es un residuo módulo q si y sólo si q es un residuo módulo p.

A esta última propiedad se le conoce como la ley de reciprocidad cuadrática, y es uno de los teoremas más importantes de la teoría elemental de números.

Problemas abiertos y conjeturas

Uno de los problemas abiertos más importantes sobre residuos cuadráticos es determinar el orden de magnitud del mínimo no-residuo cuadrático positivo n(p). El mejor resultado conocido, debido a Burguess, asegura que la expresión

está acotada para todos los primos, y se conjetura que el resultado podría seguir siendo cierto si sutituimos el denominador por (logp)².

Extensiones

Al igual que de residuos cuadráticos, podemos hablar de residuos cúbicos, residuos bicuadráticos y en general de residuos potenciales.