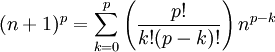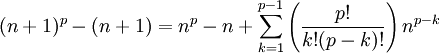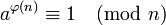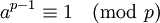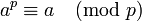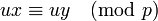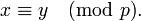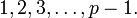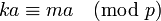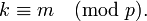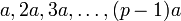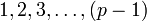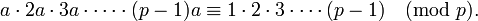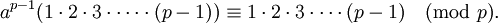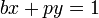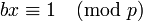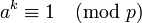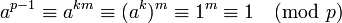En este artículo se recogen unas cuantas pruebas del pequeño teorema de Fermat, que establece:

Si a es un número natural y p un número primo, entonces ap ≡ a (mod p).

Este teorema es un caso especial del teorema de Euler que generaliza este concepto mucho más.

Contenido 1 Prueba original de Euler 2 Prueba usando el teorema de Euler 3 Prueba utilizando aritmética modular 4 Prueba utilizando teoría de grupos 5 Véase también 6 Referencias 7 Enlaces externos

Prueba original de Euler

Leonhard Euler dio en 1736 la primera demostración en un artículo titulado Theorematum Quorundam ad Números Primos Spectantium Demonstratio^[1] y es la siguiente:

Se demuestra por inducción matemática sobre los números naturales.

Sea n = 1, sabemos que 1^p -1 = 0 es divisible por p primo. Supongamos ahora que se aplica para 2 y es correcto, entonces tendremos que p|2^p -2. Si se aplica a todos los números hasta n y se cumple la proposición, y se puede demostrar que para n + 1 también se cumple, entonces se cumplirá para todo n.

• Partimos de que

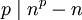
• Utilizamos el binomio de Newton para expandir la potencia (n + 1)^p:

• Agrupando factores y reordenando la identidad:

• Dado que el número resultante del sumatorio del miembro de la derecha es divisible por p, porque el coeficiente binomial 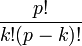es divisible por p para 0 < k < p y p primo, y n^p -n es divisible por p por hipótesis inductiva, tenemos que (n + 1)^p -(n + 1) es divisible por p.

• Repitiendo el proceso vemos que se cumple para todo n.

Prueba usando el teorema de Euler

El pequeño teorema de Fermat se puede demostrar como un caso particular del teorema de Euler. Si a es un número coprimo con n, entonces:

donde φ(n) es la función φ de Euler. Dado que para cada primo p, φ(p) = p - 1, entonces obtenemos que

que es la forma en la que se suele representar el teorema. Para obtener la forma original, solo debemos conocer una sencilla propiedad en aritmética modular que dice que si A, B son dos números enteros cualesquiera tales que A ≡ B (mod n), entonces para cualquier número natural C tenemos que AC ≡ BC (mod n).

Multiplicando a en ambos lados de la relación de equivalencia obtenemos la forma original:

Prueba utilizando aritmética modular

Esta prueba^[2] se basa en el uso de aritmética modular y es la que suele aparecer en los textos de teoría de números. La prueba se basa en dos lemas que se exponen a continuación:

Lema 1: Ley de cancelación.

Si u, x e y son números enteros y u no es divisible por un número primo p, y

entonces nosotros podemos "cancelar" u, quedando

Se puede comprobar fácilmente esto ya que según el lema de Euclides, si un primo p divide al producto rs (donde r y s son enteros), entonces p divide a r ó p divide a s. Dado que ux ≡ uy (mod p) significa que p divide a ux - uy, sacando factor común, u(x - y), y puesto que p no divide a u, tenemos que p divide a (x - y) de lo que se sigue que x ≡ y (mod p).

Lema 2: Propiedad de reagrupación.

La secuencia

con p no divisible por a, cuando es reducida módulo p , puede volver a reagruparse en la secuencia

Para empezar, ninguno de los términos a, 2a, ..., (p − 1)a puede ser cero módulo p, ya que si k es uno de los números 1, 2, ..., p − 1, entonces k no es divisible por p, y tampoco por a, así que, según el lema de Euclides ka no es divisible por p. Por lo tanto, los números de la secuencia a, 2a, ..., (p − 1)a, al ser reducidos módulo p, deben encontrarse entre los números 1, 2, 3, ..., p − 1.

Ahora bien, los números a, 2a, ..., (p − 1)a deben de ser todos distintos al ser reducidos módulo p, puesto que si

donde k y m son números de la lista 1, 2, ..., p − 1, entonces la ley de cancelación dice que

Al reducir la secuencia a, 2a, ..., (p − 1)a módulo p, obtendremos la secuencia 1, 2, ..., p − 1, pero en distinto orden, en definitiva, una biyección.

Prueba.

• Sea a un entero positivo no divisible por p. Escribimos la secuencia de números

• Si se reduce cada elemento de la secuencia módulo p y se reagrupa (lema 2), nos queda la secuencia:

• Multiplicando todos los elementos de la primera secuencia, se observa que es equivalente módulo p a la multiplicación de todos los elementos de la segunda secuencia, o sea:

• Agrupando los términos a:

• Finalmente, cancelando (lema 1) los números 1, 2 , ..., p - 1 obtenemos:

Prueba utilizando teoría de grupos

Esta prueba requiere los más básicos elementos de teoría de grupos.

La idea fundamental es reconocer que el grupo G={1, 2, …, p − 1}, con la operación de multiplicación (bajo módulo p) forma un grupo. Generalmente se denota a este grupo como (Z/nZ)^x. El único axioma de grupo que requiere un poco esfuerzo de probar es que cada elemento de G es invertible. Se prueba a continuación.

Propiedad de invertibilidad.

Para probar que cada elemento b de G es invertible, se procede de la siguiente manera. Puesto que b es coprimo con p, la identidad de Bézout asegura que existen dos enteros x e y tales que:

Leyendo esta ecuación "módulo p", se puede observar que x es el inverso de b (módulo p), puesto que

Como para cada b ∈ G existe un x que es su inverso módulo p, de concluye que G es un grupo.

Una vez demostrado que G es un grupo se prueba el teorema:

• Sea a un número entre 1 ≤ a ≤ p − 1, esto es, un elemento de G. Sea k el orden de a, así pues

• Por el teorema de Lagrange, k divide el orden de G, que es p - 1, así que p - 1=km para algún entero m. Luego

Véase también

• Pequeño teorema de Fermat
• Teorema de Euler

Referencias

• [E054] Leonhard, Euler, Theorematum quorundam ad números primos spectantium demonstratio. Commentarii academiae scientiarum Petropolitanae 8, 1741, pp. 141-146, Reprinted in Opera Omnia: Series 1, Volume 2, pp. 33 - 37.

Enlaces externos

1. ↑ Euler, Leonhard, Theorematum Quorundam ad Numeros Primos Spectantium Demonstratio (traducción paralela del latín al inglés)
2. ↑ Proof of Fermat's Little Theorem