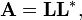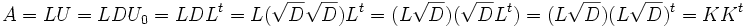En matemáticas, la factorización o descomposición de Cholesky toma su nombre del matemático André-Louis Cholesky, quien encontró que una matriz simétrica definida positiva puede ser descompuesta como el producto de una matriz triangular inferior y la traspuesta de la matriz triangular inferior. La matriz triangular inferior es el triángulo de Cholesky de la matriz original positiva definida. El resultado de Cholesky ha sido extendido a matrices con entradas complejas. Es una manera de resolver sistemas de ecuaciones matriciales y se deriva de la factorización LU con una pequeña variación.

Cualquier matriz cuadrada A con pivotes no nulos puede ser escrita como el producto de una matriz triangular inferior L y una matriz triangular superior U; esto es llamada la factorización LU. Sin embargo, si A es simétrica y definida positiva, se pueden escoger los factores tales que U es la transpuesta de L, y esto se llama la descomposición o factorización de Cholesky. Tanto la descomposición LU como la descomposición de Cholesky son usadas para resolver sistemas de ecuaciones lineales. Cuando es aplicable, la descomposición de Cholesky es dos veces más eficiente como la descomposición LU.

Contenido 1 Definición 2 Aplicaciones 2.1 Mínimos cuadrados lineales 2.2 Simulación de Monte Carlo 2.3 Filtro de Kalman 3 Véase también

Definición

En general, si A es Hermitiana y definida positiva, entonces A puede ser descompuesta como

donde L es una matriz triangular inferior con entradas diagonales estrictamente positivas, y L^* representa la conjugada traspuesta de L. Esta es la descomposición de Cholesky.

La descomposición de Cholesky es única: dada una matriz Hermitiana positiva definida A, hay una única matriz triangular inferior L con entradas diagonales estrictamente positivas tales que A = LL^*. El recíproco se tiene trivialmente: si A se puede escribir como LL^* para alguna matriz invertible L, triangular inferior o no, entonces A es Hermitiana y definida positiva.

El requerimento de que L tenga entradas diagonales estrictamente positivas puede extenderse para el caso de la descomposición en el caso de ser semidefinida positiva. La proposición se lee ahora: una matriz cuadrada A tiene una descomposición de Cholesky si y sólo si A es Hermitiana y semidefinida positiva. Las factorizaciones de Cholesky para matrices semidefinidas positivas no son únicas en general.

En el caso especial que A es una matriz positiva definida simétrica con entradas reales, L se puede asumir también con entradas reales. Una Matriz D diagonal con entradas positivas en la diagonal, es factorizable como 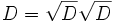, donde 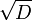es matriz cuya diagonal consiste en la raíz cuadrada de cada elemento de D, que tomamos como positivos. Así:

La factorización puede ser calculada directamente a través de las siguientes fórmulas (en este caso realizamos la factorizacón superior A = U^t * U):
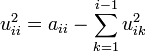para los elementos de la diagonal principal, y:

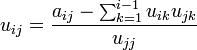para el resto de los elementos. Donde u_ij son los elementos de la matriz U.

Aplicaciones

La descomposición de Cholesky se usa principalmente para hallar la solución numérica de ecuaciones lineales Ax = b. Si A es simétrica y positiva definida, entonces se puede solucionar Ax = b calculando primero la descomposición de Cholesky A = LL^T, luego resolviendo Ly = b para y, y finalmente resolviendo L^Tx = y para x.

Mínimos cuadrados lineales

Sistemas de la forma Ax = b con A simétrica y definida positiva aparecen a menudo en la práctica. Por ejemplo, las ecuaciones normales en problemas de mínimos cuadrados lineales son problemas de esta forma. Podría ocurrir que la matriz A proviene de un funcional de energía el cual debe ser positivo bajo consideraciones físicas; esto ocurre frecuentemente en la solución numérica de ecuaciones diferenciales parciales.

Simulación de Monte Carlo

La descomposición de Cholesky se usa comúnmente en el método de Monte Carlo para simular sistemas con variables múltiples correlacionadas: La matriz de correlación intra variables es descompuesta, para obtener la triangular inferior L. Aplicando ésta a un vector de ruidos simulados incorrelacionados, u produce un vector Lu con las propiedades de covarianza del sistema a ser modelado.

Filtro de Kalman

Los filtros de Kalman usan frecuentemente la descomposición de Cholesky para escoger un conjunto de puntos sigma. El filtro de Kalman sigue el estado promedio de un sistema como un vector x de longitud N y covarianza dada por una matriz P de tamaño N-by-N. La matriz P es siempre positiva semidefinida y puede descomponerse como LL^T. Las columnas de L puede ser adicionadas y restadas de la media x para formar un conjunto de 2N vectores llamados los puntos sigma. Estos puntos sigma capturan la media y la covarianza del estado del sistema.

Véase también

• Factorización