Contenido 1 Isomorfismo canónico 1.1 Definición y teorema 1.2 Prueba 2 Descomposición de una aplicación lineal 3 Ejemplos

Isomorfismo canónico

Definición y teorema

Sean E y F dos espacios vectoriales sobre un mismo cuerpo, o más generalmente, dos módulos sobre un mismo anillo.
Sea f una aplicación lineal, N = Ker f su núcleo e I = Im f su imagen, o codominio.

Teorema: Existe un isomorfismo canónico φ:

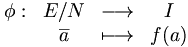
donde 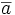= â = a + N se puede ver como la clase de a en E/N (a módulo N) o como el conjunto a + N = { a + n, n ∈ N} de los elementos de la forma a + n, con n ∈ N.

Prueba

1) Primero hay que verificar que φ está bien definida, porque se ha definido φ(â) escogiendo un elemento a (un representante) de la clase â, y mirando su imagen por f. Hay que establecer que esta imagen no depende de esta elección.
Sea entonces u∈â otro elemento de â. Las clases de a y u son idénticas: â = û, lo que se puede escribir también: a + N = u + N. Entonces u - a + N = N, lo que significa que u - a ∈ N (porque n∈ N, luego a - u + 0 también).
Luego existe n en el núcleo de f tal que u = a + n. entonces f(u) = f(a + n) = f(a) + f(n) = f(a) + 0 = f(a) por linealidad.

2) φ es sobreyectiva: Todo elemento de la imagen I es por definición de la forma f(a) que vale φ(â); luego pertenece también a Im φ.

3) φ es inyectiva: φ(â) = 0 significa que f(a) = 0, es decir que a∈N. entonces â = a + N = o + N = N = ô que es el elemento neutro de E/N.

Descomposición de una aplicación lineal

Este isomorfismo se completa naturalmente en una descomposición de f: f = i°φ°π, donde i es la inclusión canónica de I en F (i(x) = x para todo x∈I ), y π es la sobreyección canónica de E sobre E/N (π(a) = â para todo a∈E):

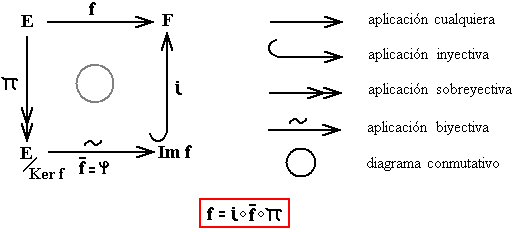
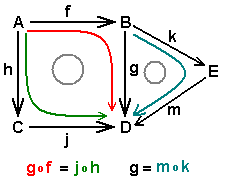
En efecto: f = i°φ°π(a) = f = i°φ(â) = i(φ(â)) = φ(â) = f(a) para todo a∈E.

El diagrama precedente es conmutativo en el sentido siguiente:
Cuando existen dos caminos para ir de un punto a otro del diagrama, respetando claro está la orientación de las flechas, entonces se obtiene el mismo resultado por la composición de las aplicaciones.
En este nuevo ejemplo, los caminos verdes y rojos dan la misma aplicación: g°f = j°h, y el camino azul equivale al negro: m°k = g.

Ejemplos

1) Sea f la aplicación que asocia a un entero n su resto por la división euclidiana por 7 (escogido al azar).
Los restos posibles son 0, 1, 2, 3, 4, 5 y 6. La división de 6 por 7 da un resto de 6, mientras que la de 7 por 7 da como resto 0. Es por lo tanto lógico decidir que 0 sucede a 6 en este conjunto, que adquiere así una estructura circular. De hecho, se trata del anillo cíclico Z₇: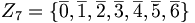

, provisto de la adición módulo 7 y de la multiplicación también módulo 7.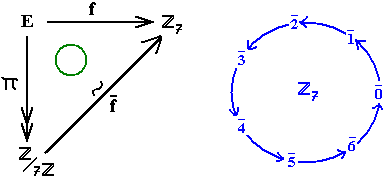

La aplicación f es lineal como propiedad de las congruencias, es sobreyectiva porque cada cifra entre 0 y 6 corresponde a un resto posible: basta con tomar el dividendo igual a la cifra.

No es inyectiva, y su núcleo es {...-21; -14; - 7; 0; 7; 14; 21...} = 7·Z, porque los dividendos que dan restos nulos son claramente los múltiplos de 7.

Como la inclusión i es, como f, sobreyectiva, se vuelve biyectiva (una inclusión es por definición inyectiva) y podemos prescindir de ella en la descomposición:

La flecha en diagonal representa el isomorfismo canónico entre Z/7Z y Z₇.

2) Consideremos el producto vectorial en R³, por un vector dado. Para fijar las cosas, sea (i, j, k) una base ortonormal directa del espacio usual, y estudiemos la aplicación que al vector u asocia el vector i × u (el producto vectorial se denota "×" o "^", según los países).

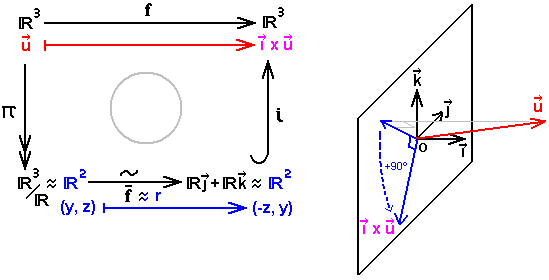
Su descomposición es la siguiente:
La sobreyección π es asimilable a la proyección ortogonal sobre el plano (Oyz) (mediante la identificación de una recta dirigida por i a su intersección con el plano anterior). En ella interviene la rotación r directa de 90 grados en el plano (Oyz) perpendicular al vector i.
De hecho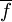 es asimilable a r (gracias a la identificación anterior).
Esto no es de extrañar porque el producto vectorial y las rotaciones en el espacio están íntimamente ligadas (ver cuaterniones y rotación en el espacio).