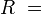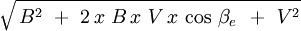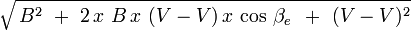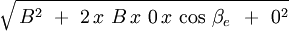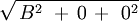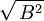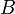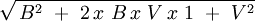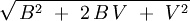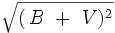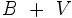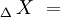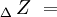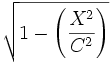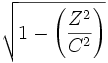Dilatación del tiempo y contracción de la longitud

Dilatación del tiempo y contracción de la longitud

Dilatación del tiempo y contracción de la longitud

Con la finalidad de comprender adecuadamente, dentro de la “Teoría de la Relatividad Especial” tanto la “Dilatación del Tiempo” como la “Contracción de la Longitud”, es necesario recapitular en el tiempo en una breve reseña histórica de la Física Clásica.

Asimismo, en la siguiente tabla podemos visualizar las diferentes "constantes" propias, que - conjuntamente con otros postulados - separan a la Física Clásica de la Física Einsteníana, y a éstas dos últimas de la Física Cuántica.

LÍMITE LUGAR de aplicación CONSTANTE APLICABLE A: VARIOS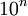
\,10^n \, Macro Constante de Einstein Velocidad de la Luz 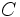\,C \,
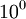
\,10^0 \, Cotidiano Constantes de Newton Tiempo ( T ), Espacio ( D ) y Movimiento ( V ) 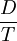\frac{D}{T} \,{= V}
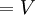
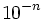
\,{10^{-n}} \, Micro Constante de Planck Energía cuántica 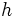\,h \,


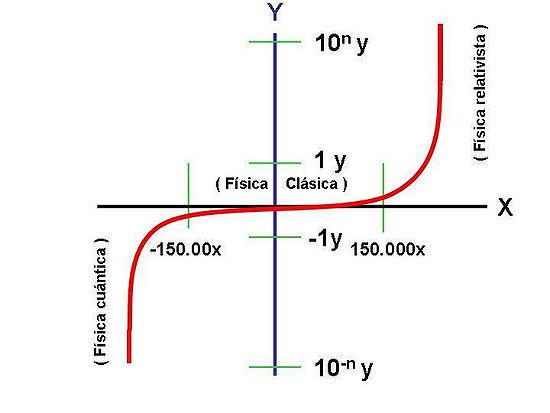
La tabla precedente la podríamos graficar utilizando la ecuación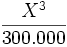 \frac{X^3}{300.000} \,{= Y}



Macro y Micro TT.jpg



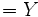
Algunos sostienen que, hasta ahora, la “Relatividad general” y la “Mecánica cuántica” son - en alguna medida - INCOMPATIBLES, considerando que si se intenta realizar algún tipo de cálculo usando simultáneamente ambas herramientas genera respuestas paradójicos, por decirlo de alguna manera. Esta eventual contradicción quedaría en evidencia cuando se intenta calcular matemáticamente la interacción de partículas en trazos cortos, como son los que se dan en la “Escala de Planck”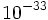 \,\,\,\,{10^{-33}} \, {cm }


Contenido

Principios y postulados de la Física clásica del Siglo XIX

Nómina de los principales principios y postulados de la Física clásica

Nº Principio o postulado de la Física Clásica Más información
1 Principio de adición de velocidades de Galileo Suma vectorial
2 Principio de Causalidad Causalidad (física)
3 Principio de razón suficiente Principio de razón suficiente
4 Principio de determinismo Principio de determinismo
5 Grados de libertad Grados de libertad (física)
6 Predictibilidad [1]
7 Éter Éter
8 Vació Absoluto Discusión:Energía del punto cero
9 Luz ondulatoria
10 Tiempo absoluto
11 Espacio absoluto
12 Todo se puede representar gráficamente Representación gráfica

Ejercicios gráfico en Física Clásica

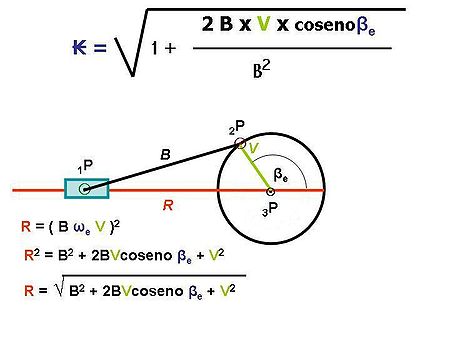
Principio de adición de velocidades de Galileo, con una longitud que no se contrae y un tiempo que no se dilata. La suma de velocidades con fasores es un método semigráfico, válido para dos objetos físicos como dos ondas que se desplazan por el “éter”, en dirección de 0º a 380º, que por lo mismo lo podemos representar por el movimiento que realiza una Biela, y por las funciones matemáticas asociadas a la sumatoria de las velocidades "V" y "B":

Biela.jpg

Gráfico de la adición de velocidades de dos objetos físicos

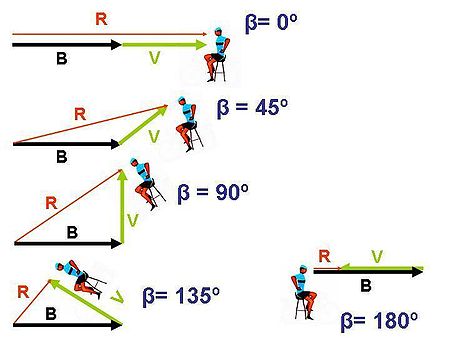
En el gráfico siguiente se visualiza la suma de velocidades para los ángulos de 0º; 45º; 90º, 135º y 180º, respectivamente:

Suma de velocidades TT.JPG


\,\,\,R \,\, = \,\, \,\,\sqrt { \,B^2\,\,+\,\,2\,x\, \,B\,x\, \,V\,x\,\cos\,\beta_e\,\,\,+\,\,V^2}

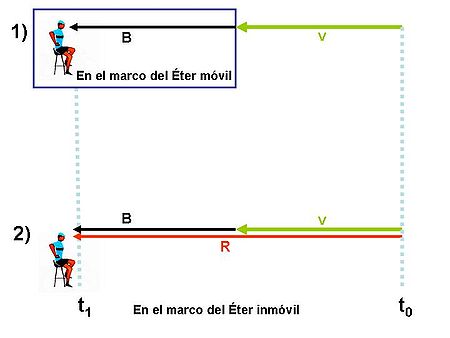
Gráfico de la adición de velocidades de ondas luminosas

Con y sin Éter movil.jpg

Según la física clásica, el sujeto del ejemplo uno se encuentra en el mismo marco de referencia del “Éter móvil”, situación que impide se percate de la adición de ambas ondas.


\,\,\,R \,\, = \,\, \,\,\sqrt { \,B^2\,\,+\,\,2\,x\, \,B\,x\, \,(V-V)\,x\,\cos\,\beta_e\,\,\,+\,\,(V-V)^2}


\,\,\,R \,\, = \,\, \,\,\sqrt { \,B^2\,\,+\,\,2\,x\, \,B\,x\, \,0\,x\,\cos\,\beta_e\,\,\,+\,\,0^2}


\,\,\,R \,\, = \,\, \,\,\sqrt { \,B^2\,\,+\,0\,+\,\,0^2}


\,\,\,R \,\, = \,\, \,\,\sqrt { \,B^2}


\,\,\,R \,\, = \,\, \,\,B


En cambio, según la misma física clásica, en el caso del observador dos, al estar situado en el marco de referencia del “Éter Inmóvil”, visualiza la adición de velocidades de ambas ondas.


\,\,\,R \,\, = \,\, \,\,\sqrt { \,B^2\,\,+\,\,2\,x\, \,B\,x\, \,V\,x\,\cos\,\beta_e\,\,\,+\,\,V^2}


\,\,\,R \,\, = \,\, \,\,\sqrt { \,B^2\,\,+\,\,2\,x\, \,B\,x\, \,V\,x\,\,1\,\,+\,\,V^2}


\,\,\,R \,\, = \,\, \,\,\sqrt { \,B^2\,\,+\,\,2\,B\,V\,\,+\,\,V^2}


\,\,\,R \,\, = \,\, \,\,\sqrt { (\,B \,\,+\,\,V)^2}


\,\,\,R \,\, = \,\, \,\,B\,\,+\,\,V

Gráfico bajo los postulados de la Relatividad

El Experimento de Michelson y Morley demostró que el Éter no existe. La relatividad, por su parte postula que, con la velocidad, el tiempo se dilata y la longitud se contrae. Asimismo, que en el vació la suma de dos ondas luminosas no pueden superar la velocidad \,\,C \,.

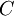Matemáticamente hablando cómo se puede graficar aquello y ¿Cómo se asocian la contracción y la dilatación para que 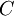\,\,C \,, sea una constante universal?

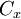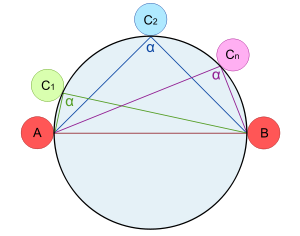
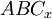Sea \,\,C_x \, \, un punto cualquiera de la circunferencia de diámetro \, [\,AB \,] \, , igual o distinto de los puntos A y de B. Entonces el triángulo \,\,ABC_x \, \, es un triángulo rectángulo.

ES-Teorema de Tales de Mileto.svg

En otras palabras, podemos manifestar que el teorema de Tales dice que si los tres vértices de un triángulo están sobre una circunferencia dada, en donde uno de sus lados siempre es el diámetro de la circunferencia; entonces el "ángulo opuesto" a éste lado es un ángulo recto.

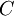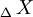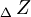El diámetro de la circunferencia, representara la velocidad de la luz \,\,C \,, y a la vez los fasores \,\,\,{_\Delta \,X}\,\, y \,\,\,{_\Delta \,Z}\,\,, representarán la dilatación y la contracción, respectivamente:


\,\,\,{_\Delta \,X} \,\, = \,\, \,\,\sqrt{C^2\,\,-\,\,\,{_\Delta\,Z^2}}


\,\,\,{_\Delta \,Z} \,\, = \,\, \,\,\sqrt{C^2\,\,-\,\,\,{_\Delta \,X^2}}


\sqrt{1-\left(\frac{X^2}{C^2}\right)}


\sqrt{1-\left(\frac{Z^2}{C^2}\right)}



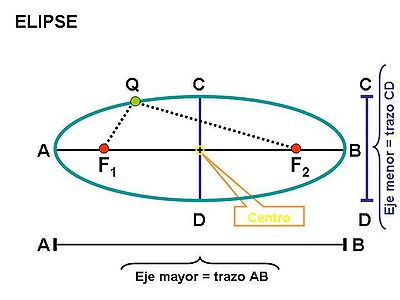
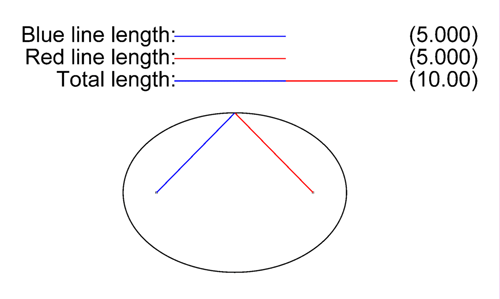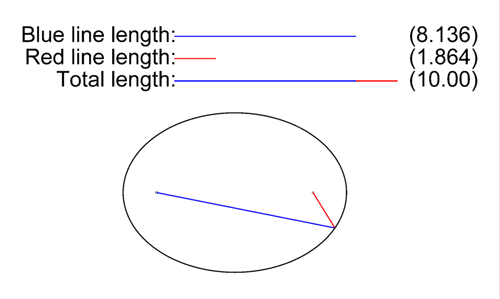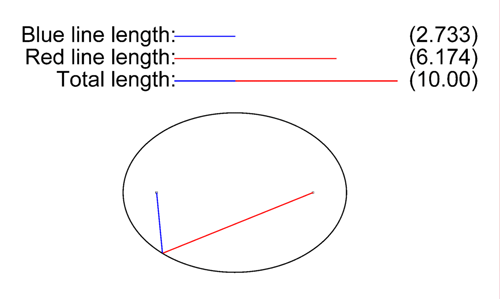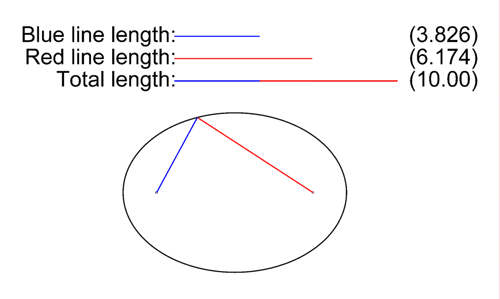
En la elipse, la longitud desde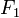 \, {F_1} al punto 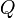\, {Q} sumada a la longitud desde 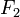\, {F_2} a ese mismo punto 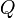\, {Q} , es una cantidad constante que siempre será igual a la longitud del «eje mayor», esto es al trazo \,\,AB \,.


WIKI elipse TT.JPG


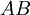En consecuencia la velocidad de la luz en el vació (constante universal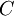 \,\,C \,), la podemos representar gráficamente por el «eje mayor» de la elipse, o trazo 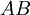\,\,AB \,. Y la sumatoria de la velocidad del foco (segmento 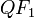\,\,QF_1 \,) con de la velocidad de la onda (segmento 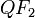\,\,QF_2 \,), no podrá superar la velocidad 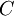\,\,C \,), aquí representada por el segmento \,\,AB \,.

Ellipse Animation Small.gif

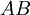Notas

Obtenido de "Dilataci%C3%B3n del tiempo y contracci%C3%B3n de la longitud"

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Historia del electromagnetismo — La Historia del electromagnetismo, que es el conocimiento y el uso registrado de las fuerzas electromagnéticas, data de hace más de dos mil años. En la antigüedad ya estaban familiarizados con los efectos de la electricidad atmosférica, en… …   Wikipedia Español

  • Contracción de Lorentz — Esquema sobre la contracción de Lorentz. (X′,cT′) representan las coordenadas de un observador en reposo a una barra, mientras que (X,cT) son las coordenadas de otro observador con respecto a dicha barra, por la naturaleza pseudoeuclídea del… …   Wikipedia Español

  • Teoría del estado estacionario — La Teoría del Estado Estacionario es un modelo cosmológico desarrollado en 1949 por Hermann Bondi, Thomas Gold y Fred Hoyle como una alternativa a la Teoría del Big Bang. Aunque el modelo tuvo un gran número de seguidores en la década de los 50,… …   Wikipedia Español

  • Teoría de la relatividad especial — Teoría de la Relatividad, parte de Walk of Ideas, en la Isla de los Museos (Berlín). Festejando el …   Wikipedia Español

  • Interferómetro de Fizeau — A). Interferómetro de Fizeau para medir la adición de la velocidad del agua con la velocidad de la luz …   Wikipedia Español

  • Física — Si he logrado ver más lejos, ha sido porque he subido a hombros de gigantes. Sir …   Wikipedia Español

  • Apotema — Saltar a navegación, búsqueda Apotema de un hexágono La apotema de un polígono regular es la distancia entre el centro y cualquiera de sus lados. Es un segmento cuyos extremos son el centro de un polígono regular y el punto medio de uno… …   Wikipedia Español

  • Lorentz-FitzGerald, contracción de — o contracción espacial En la física de la relatividad, el acortamiento de la longitud de un objeto en la dirección de su movimiento relativo al observador. Las dimensiones en las otras direcciones no se contraen. Este concepto fue propuesto por… …   Enciclopedia Universal

  • Experimento de Michelson y Morley — Saltar a navegación, búsqueda El experimento de Michelson y Morley fue uno de los más importantes y famosos de la historia de la física. Realizado en 1887 por Albert Abraham Michelson y Edward Morley, está considerado como la primera prueba… …   Wikipedia Español

  • Historia de la Relatividad Especial — La teoría de la relatividad surge para resolver varios problemas con las teorías aceptadas al principio del siglo XX. Contenido 1 La relatividad anterior a 1900 2 Nuevas transformaciomes del movimiento 3 Eventos hasta la formulación de la… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”