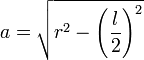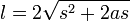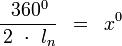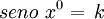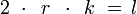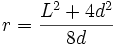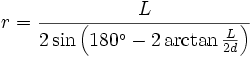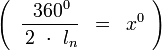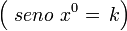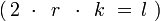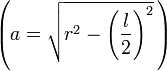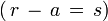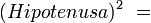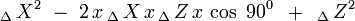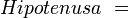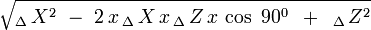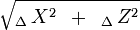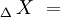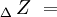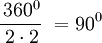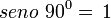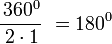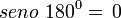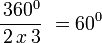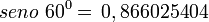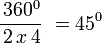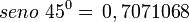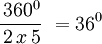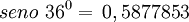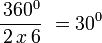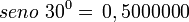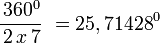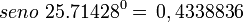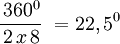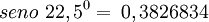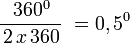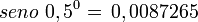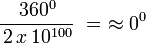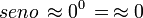Apotema

Apotema

Apotema

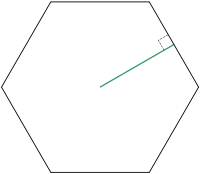Apotema de un hexágono

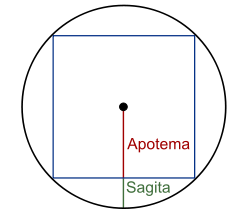
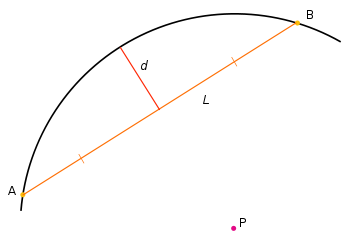
La apotema de un polígono regular es la distancia entre el centro y cualquiera de sus lados. Es un segmento cuyos extremos son el centro de un polígono regular y el punto medio de uno cualquiera de sus lados, y es siempre perpendicular a dicho lado.

En una pirámide regular, también se denomina apotema al segmento trazado desde el vértice al centro de cualquier lado del polígono que conforma la base; coincide con la altura de cada cara triangular de la pirámide regular.

Contenido

Apotema y Sagita

Apotema y Sagita.svg

El radio se subdivide en dos segmentos: la apotema y la sagita; así, podemos decir que el complemento de la apotema es la sagita, cuya unión es el radio.

Principales medidas asociadas a la apotema y a la sagita

Formulas de la Apotema y de la Sagita.
  • Sea 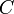\,C una circunferencia de centro \, O
De «radio» \,r = OQ
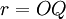
Y sea 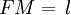\,FM = \, l uno de los lados del polígono regular inscrito de 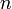\,n lados, cuyo perímetro conocemos.
De «apotema» \,a = OK
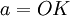
De «sagita» \,s = KQ
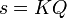
  • Lado del polígono: \, = l
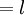
  • Apotema: \, = a
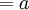
  • Sagita: 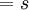\, = s *Radio: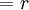 \, = r
  • Perímetro del polígono: \, = P.
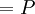  • Área del polígono: \, = A.
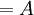  • Cantidad de lados: \,n.
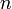Entonces:
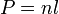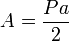
\,P = nl, y A = \frac{Pa}{2}

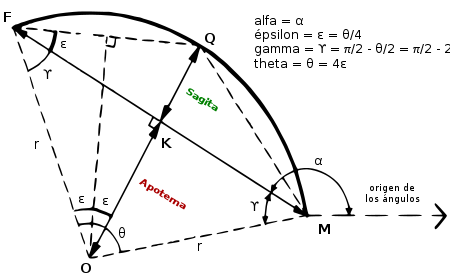
El diccionario Larouse define Sagita como la parte del radio comprendida entre el punto medio de un arco de círculo y el de su cuerda

Formulas

Entonces la apotema 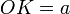\,OK = a , viene dada por la formula:

a = \sqrt{r^2-\left(\frac{l}{2}\right)^2}

Por lo tanto una vez calculado el valor de la apotema podemos conocer el valor de la sagita 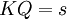\,KQ = s , toda vez que \,s = r - a .

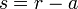Por su parte el segmento 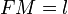\,FM = l del polígono regular inscrito se puede calcular a partir de la formula:

l = 2\sqrt{s^2+2as}


Si se desconoce el valor, tanto de la apotema (a) como de la sagita (s), entonces la longitud del segmento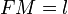 \,FM = l , se puede calcular a partir de la formula:


\,\,\,\,\, \frac {\,360^0} {\,2\,\, \cdot \,\, l_n}\,\, \, = \,\,\,x^0\,\,


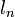En donde \,\, l_n\,\, \,, es la cantidad de lados que tiene el polígono regular inscrito.


\, \,seno \, \,x^0 = \,k


\,2 \,\,\cdot \,\,\,r \,\,\, \cdot \,\,\,k \, \, = \,l\,\,

En general para el arco de un círculo

Determinando el radio a partir de una cuerda y un arco.

Es posible también determinar el radio del círculo cuando se proporciona un arco, si se conoce la longitud 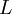\,L de una cuerda, y a la vez, la distancia 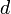\,d que hay del punto medio de la cuerda al punto medio del arco determinado por la cuerda usando la fórmula:

r = \frac{ L^2 + 4d^2}{8d}

o la ecuación trigonométrica:

r = \frac{L}{2 \sin\left(180^\circ - 2 \arctan \frac{L}{2d}\right)}

En donde:

un lado del polígono 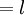\, = l, es la longitud 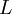\, L (véase imagen).
y la sagita 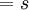\, = s, es la distancia \,d.

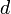Cálculo de la "apotema" y de la "sagita" en diferentes polígonos regulares

Un polígono cuyos lados tienen la misma longitud y todos sus ángulos[1] internos son iguales, se llama polígono regular, lo que implica que, la magnitud de la apotema del «polígono rectangular» subsiguiente, no es una cantidad continua sino que es a «saltos progresivos».


\,\,\left (\,\,\, \frac {\,360^0} {\,2\,\, \cdot \,\, l_n}\,\, \, = \,\,\,x^0\,\,\right)


\left (\, \,seno \, \,x^0 = \,k \right)


\left (\,2 \,\,\cdot \,\,\,r \,\,\, \cdot \,\,\,k \, \, = \,l\,\,\right)


\left (a = \sqrt{r^2-\left(\frac{l}{2}\right)^2}\, \right)


\left (\,r \,- \,a \, = \,s \right)


En donde:
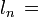\, l_n \, = \,\, cantidad de lados del polígono regular.
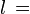\, l\, = \,\, longitud del cada lado del polígono regular.
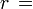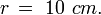\, r \, = \,\, radio de la circunferencia ( Para todos los ejercicios siguientes el radio \,\,\, r \, = \,\,10\,\,cm.\,\,)
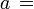\, a \, = \,\, apotema.
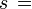\, s \, = \,\, sagita.


Caso especial

Si consideramos:

  • Que, todo triángulo tiene tres lados
  • Que, en la geometría euclidiana, los tres ángulos internos de un triángulo miden 180°
  • Que, existen ángulos, tanto de de 0º como de 90º

Entonces, nos encontramos legitimados para hacer un «Gedankenexperiment», en donde uno de los ángulos internos del triángulo mida 0º, y los dos restantes 90º cada uno. En tal evento, uno de los lados del triángulo medirá 0 cm., y los dos restantes tienen el diámetro de la circunferencia. En ese triángulo, así confeccionado, visualizaremos dos de sus lados traslapados. Con ello no violamos ninguno de los postulados precedentes.

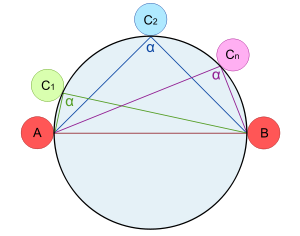
Confirma lo anterior el «segundo teorema de Tales de Mileto»: «Todo ángulo inscrito en un semicírculo es un ángulo recto.»


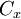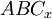Sea \,\,C_x \, \, un punto cualquiera de la circunferencia de diámetro \, [\,AB \,] \, , igual o distinto de los puntos A y de B. Entonces el triángulo \,\,ABC_x \, \, siempre será un triángulo rectángulo.


ES-Teorema de Tales de Mileto.svg


En otras palabras, podemos manifestar que el teorema de Tales dice que si los tres vértices de un triángulo están sobre una circunferencia dada, en donde uno de sus lados siempre es el diámetro de la circunferencia; entonces el "ángulo opuesto" a éste lado es un ángulo recto.


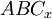  • El segmento \left [\,AB \, \right] es el diámetro de la circunferencia. Diámetros que, para el triángulo rectángulo inscrito \,\,ABC_x \, \, , será la hipotenusa con carácter invariante.
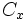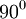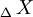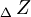  • Asimismo existe otra constante, según ya lo señalamos, dado que los fasores en el punto \,\,\,C_x\,\,, siempre tienen \,\,\,90^0\,\,, debemos aplicar la ley de los cosenos, en donde \,\,\,{_\Delta\,X}\,\, y \,\,\,{_\Delta \,Z}\,\, son los fasores (véase arco capaz):


\,\,\,(Hipotenusa)^2 \,\, = \,\, \,\,{_\Delta \,X^2}\,\,-\,\,2\,x\,{_\Delta \,X}\,x\,{_\Delta \,Z}\,x\,\cos\,\,90^0\,\,\,+\,\,\,{_\Delta \,Z^2}


\,\,\,Hipotenusa \,\, = \,\, \,\,\sqrt {{_\Delta \,X^2}\,\,-\,\,2\,x\,{_\Delta \,X}\,x\,{_\Delta \,Z}\,x\,\cos\,\,90^0\,\,\,+\,\,\,{_\Delta \,Z^2}}


Considerando que toda cantidad multiplicada por cero es cero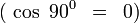 (\,\,\cos \,\,90^0 \,\,\,=\,\,\,0 ), podemos eliminar de la ecuación esta parte: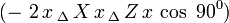 \,(-\,\,2\,x\,{_\Delta \,X}\,x\,{_\Delta \,Z}\,x\,\cos\,\,90^0)


\,\,\,Hipotenusa \,\, = \,\, \,\,\sqrt {{_\Delta \,X^2}\,\,\,+\,\,\,{_\Delta \,Z^2}}


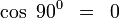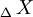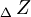Nota: La longitud de la hipotenusa, para este caso, siempre será igual al diámetro de la circunferencia, y a la vez \,\,\cos \,\,90^0 \,\,\,=\,\,\,0 , de manera tal que la longitud variable de los fasores \,\,\,{_\Delta \,X}\,\, y \,\,\,{_\Delta \,Z}\,\,, son calculables - para cualquiera que sea la ubicación del punto 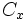\,\,\,C_x\,\, - ya sea por las formulas trigonometricas, o a través del teorema de Pitágoras:


\,\,\,{_\Delta \,X} \,\, = \,\, \,\,\sqrt{H^2\,\,-\,\,\,{_\Delta\,Z^2}}


\,\,\,{_\Delta \,Z} \,\, = \,\, \,\,\sqrt{H^2\,\,-\,\,\,{_\Delta \,X^2}}
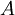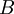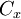  • Los puntos \, \,A \,\,\, ; \,\,B \,\,\,\, y \,\,\,C_x \,\,\, al ser traslapados por el perímetro de la circunferencia, son puntos «cocíclicos».
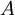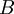  • Si un nodo es punto que permanece fijo para un determinado marco de referencia, entonces, los puntos \,\,\,A \,\,\,\, y \,\,\,B \,\,\,\, son nodos equidistantes entre sí, que además dividen la circunferencia en dos semicírculos.
  • El punto 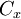\,\,C_x \,\,\,\, puede estar en cualquier lugar del perímetro de cualquiera de ambos semicírculo, incluso traslapando al punto 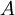\,\,\,A \, \, o al punto \,\,B \, \,.
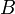  • La longitud de un cateto tiende a cero cuando su ángulo adyacente tiende a cero. Y en contra partida, la longitud del otro cateto tiende a igualar el valor de la hipotenusa.

Todo lo expuesto anteriormente, nos permite iniciar el cálculo del apotema y de la sagita, para este caso especial:


\, \frac {\,360^0} {\,2\cdot 2} \, \, = 90^0


\,seno \, \,90^0 = \,1


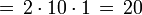
Longitud de cada lado traslapado = \,2 \cdot 10 \cdot 1 \, = \, 20\,


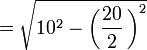
Apotema = \sqrt{10^2-\left(\frac{20}{2}\,\right)^2}\, \,= \, \,0


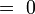
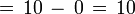
Sagita \,= \,10 \,- \,0 \, = \,10 \,

Este caso especial encierra una paradoja, puesto que: ¡no estamos en presencia de un polígono regular inscrito!, y no obstante su inexistencia, pudimos calcular sin dificultad la “sagita” y la “apotema”. ¿La apotema y la sagita serán ajenas a los polígonos regulares inscritos?

Visualicemos, en este caso especial, qué propiedades del “polígono regular inscrito” se han cumplido y cuáles no:

  1. Todos los vértices del polígono regular inscrito son puntos cocíclicos: se cumple esta propiedad, ya que el perímetro de la circunferencia toca los puntos \,\,A \, \, ; \,\,B \, \, y \,\,C_x \, \,.
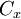  2. El centro de un polígono regular es un punto equidistante de todos los vértices del polígono: También se cumple esta propiedad, porque el centro del polígono traslapa el centro de la circunferencia que lo inscribe.
  3. Todos los puntos cocíclicos del polígono regular inscrito son equidistantes, y dividen, el perímetro de la circunferencia, en partes iguales: ¿se cumple o no esta propiedad?, el punto 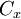\,\,C_x \, \, traslapa al punto 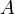\,\,A \, \,, tienen la misma ubicación, por lo que son equidistantes entre sí; ambos puntos están, entre sí, a una distancia cero, pero la distancia al punto 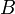\,\,B \, \, es diferente a cero. 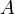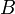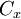Los puntos \,\,A \, \, ; \,\,B \, \, y \,\,C_x \, \,, dividen el perímetro de la circunferencia en dos partes iguales, cuando en el hecho tres puntos la debieran dividir en tres porciones.
  4. Los polígonos regulares son equiláteros; todos sus lados tienen la misma longitud: no se cumple, dado que uno de los lados del polígono tiene una longitud de 0, y los dos restante tienen por longitud el diámetro de la circunferencia.
  5. Todos los ángulos interiores de un polígono regular tienen la misma medida, es decir, son congruentes: no se cumple, porque uno tiene 0º y los dos restantes 90º.

Disquisiciones

Al parecer, para calcular la “apotema” y la “sagita” es suficiente con considerar la cantidad de puntos cocíclicos, los que pueden ir desde uno hasta infinito. En efecto, 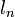\,\, l_n\,\, \, será la cantidad de puntos cocíclicos.


\,\,\,\,\, \frac {\,360^0} {\,2\,\, \cdot \,\, l_n}\,\, \, = \,\,\,x^0\,\,


Y para este caso, consideraremos que tenemos un solo punto cocíclico.


\, \frac {\,360^0} {\,2 \cdot 1} \, \, = 180^0


\,seno \, \,180^0 = \,0


Longitud, en línea recta, que separa a cada punto cocíclico, para este caso es 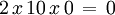\,2 \,x \,10 \,x \,0 \, = \, 0\,, dado que, en este ejemplo, tenemos solamente un punto.


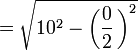
Apotema = \sqrt{10^2-\left(\frac{0}{2}\,\right)^2}\, \,= \, \,10


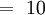
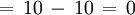
Sagita \,= \,10 \,- \,10 \, = \,0 \,

Polígono regular de tres lados (Triángulo) inscrito.

\, \frac {\,360^0} {\,2\,x\,3} \, \, = 60^0


\,seno \, \,60^0 = \,0,866025404


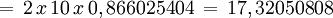
Longitud de cada lado del polígono regular = \,2 \,x \,10 \,x \,0,866025404 \, = \, 17,32050808\,


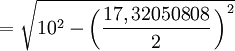
Apotema = \sqrt{10^2-\left(\frac{17,32050808}{2}\,\right)^2}\, \,= \, \,5


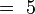
Sagita \,= \,10 \,- \,5 \, = \,5 \,

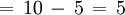
Polígono regular de cuatro lados (Cuadrilátero) inscrito.

\, \frac {\,360^0} {\,2\,x\,4} \, \, = 45^0


\,seno \, \,45^0 = \,0,7071068


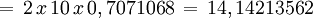
Longitud de cada lado del polígono regular = \,2 \,x \,10 \,x \,0,7071068 \, = \, 14,14213562\,


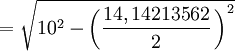
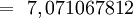
Apotema = \sqrt{10^2-\left(\frac{14,14213562}{2}\,\right)^2}\, \,= \, \,7,071067812


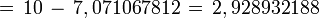
Sagita \,= \,10 \,- \,7,071067812 \, = \,2,928932188 \,

Polígono regular de cinco lados (Pentágono) inscrito.

\, \frac {\,360^0} {\,2\,x\,5} \, \, = 36^0


\,seno \, \,36^0 = \,0,5877853


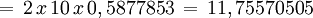
Longitud de cada lado del polígono regular = \,2 \,x \,10 \,x \,0,5877853 \, = \, 11,75570505\,


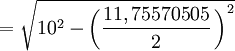
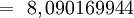
Apotema = \sqrt{10^2-\left(\frac{11,75570505}{2}\,\right)^2}\, \,= \, \,8,090169944


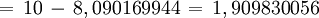
Sagita \,= \,10 \,- \,8,090169944 \, = \,1,909830056 \,

Polígono regular de seis lados (Hexágono) inscrito.

\, \frac {\,360^0} {\,2\,x\,6} \, \, = 30^0


\,seno \, \,30^0 = \,0,5000000


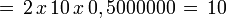
Longitud de cada lado del polígono regular = \,2 \,x \,10 \,x \,0,5000000 \, = \, 10\,


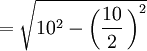
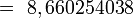
Apotema = \sqrt{10^2-\left(\frac{10}{2}\,\right)^2}\, \,= \, \,8,660254038


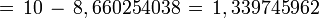
Sagita \,= \,10 \,- \,8,660254038 \, = \,1,339745962 \,

Polígono regular de siete lados (Heptágono) inscrito.

\, \frac {\,360^0} {\,2\,x\,7} \, \, = 25,71428^0


\,seno \, \,25.71428^0 = \,0,4338836


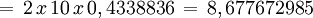
Longitud de cada lado del polígono regular = \,2 \,x \,10 \,x \,0,4338836 \, = \, 8,677672985\,


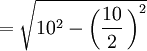
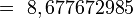
Apotema = \sqrt{10^2-\left(\frac{10}{2}\,\right)^2}\, \,= \, \,8,677672985


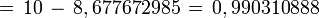
Sagita \,= \,10 \,- \,8,677672985 \, = \,0,990310888 \,

Polígono regular de ocho lados (Octágono) inscrito.

\, \frac {\,360^0} {\,2\,x\,8} \, \, = 22,5^0


\,seno \, \,22,5^0 = \,0,3826834


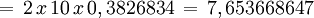
Longitud de cada lado del polígono regular = \,2 \,x \,10 \,x \,0,3826834 \, = \, 7,653668647\,


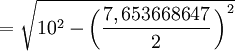
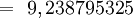
Apotema = \sqrt{10^2-\left(\frac{7,653668647}{2}\,\right)^2}\, \,= \, \,9,238795325


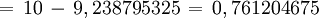
Sagita \,= \,10 \,- \,9,238795325 \, = \,0,761204675 \,

Polígono regular de 360 lados inscrito.

\, \frac {\,360^0} {\,2\,x\,360} \, \, = 0,5^0


\,seno \, \,0,5^0 = \,0,0087265


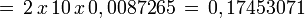
Longitud de cada lado del polígono regular = \,2 \,x \,10 \,x \,0,0087265 \, = \, 0,17453071\,


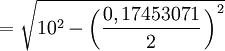
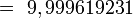
Apotema = \sqrt{10^2-\left(\frac{0,17453071}{2}\,\right)^2}\, \,= \, \,9,999619231


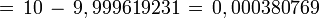
Sagita \,= \,10 \,- \,9,999619231 \, = \,0,000380769 \,

Polígono regular Gugólgono inscrito.

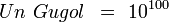
\,Un \,\,Gugol\,\,\, = \,\,10^{100}


En este caso, la gran cantidad de lados del polígono regular tiende al infinito, y se asemeja más a una circunferencia, por lo que la sagita tiende a cero y la apotema a la longitud del radio.

\, \frac {\,360^0} {\,2\,x\,10^{100}} \, \, = \, \, \approx 0^0


\,seno \, \approx 0^0 \, = \,\approx 0


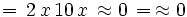
Longitud de cada lado del polígono regular = \,2 \,x \,10 \,x \, \approx 0\, = \, \approx 0\,


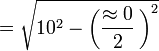
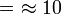
Apotema = \sqrt{10^2-\left(\frac{\approx 0}{2}\,\right)^2}\, \,= \, \,\approx 10


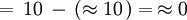
Sagita \,= \,10 \,- \,(\approx 10 \,) = \,\approx 0 \,

Y si se trata de un gúgolplex, mucho mejor pues en más grande que un Gúgol. Pero, aun así un gúgolplex no deja de ser finito.

Obtenido de "Apotema"

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • apotemă — APOTÉMĂ, apoteme, s.f. Perpendiculară dusă din centrul unei poligon regulat pe mijlocul oricăreia dintre laturile sale. ♦ Dreaptă dusă din vârful unei piramide regulate pe mijlocul oricăreia dintre laturile bazei. – Din fr. apothème. Trimis de… …   Dicționar Român

  • apotema — ‘Perpendicular que va desde el centro de un polígono regular a uno cualquiera de los lados’ y ‘altura de las caras triangulares de una pirámide regular’: «¿Cuánto mide la apotema de un pentágono regular de lado 10 cm?» (VV. AA. Matemáticas [Esp.… …   Diccionario panhispánico de dudas

  • apótema — s. m. 1. Perpendicular tirada do centro de um polígono regular a um dos lados. 2. Precipitado que se forma nas dissoluções dos extratos vegetais …   Dicionário da Língua Portuguesa

  • apotema — apotéma ž DEFINICIJA mat. okomica spuštena iz središta pravilnog poligona ili pravilnog poliedra na stranicu ili pobočnu plohu ETIMOLOGIJA fr. apothème ≃ grč. hypóthema: osnova …   Hrvatski jezični portal

  • apotema — sustantivo femenino 1. Área: geometría Línea perpendicular trazada desde el centro de un polígono regular a cualquiera de sus lados. 2. Área: geometría Altura de las caras triangulares de una pirámide regular …   Diccionario Salamanca de la Lengua Española

  • apotema — (Del gr. ἀποτιθέναι, deponer, bajar). 1. f. Geom. Distancia entre el centro de un polígono regular y uno cualquiera de sus lados. 2. Geom. Altura de las caras triangulares de una pirámide regular …   Diccionario de la lengua española

  • apotema — (Del gr. apo, desde + tithemi, colocar.) ► sustantivo femenino 1 GEOMETRÍA Perpendicular trazada desde el centro de un polígono regular a cualquiera de sus lados. 2 GEOMETRÍA Altura de las caras triangulares de una pirámide regular. * * * apotema …   Enciclopedia Universal

  • apotema — {{＃}}{{LM A03037}}{{〓}} {{［}}apotema{{］}} ‹a·po·te·ma› {{《}}▍ s.f.{{》}} Línea perpendicular trazada desde el centro de un polígono regular a cualquiera de sus lados: • La apotema de este pentágono une su centro con el punto medio de uno de sus… …   Diccionario de uso del español actual con sinónimos y antónimos

  • apotema — f Desde el centro de cualquier polнgono regular, perpendicular trazada a la mitad de cualquiera de sus lados …   Diccionario de Construcción y Arquitectur

  • apotema — a|po|te|ma Mot Pla Nom femení …   Diccionari Català-Català

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”