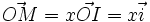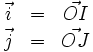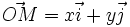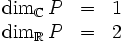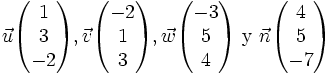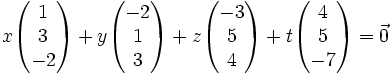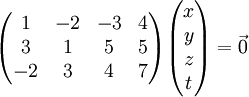La dimensión de un espacio vectorial es la respuesta a la pregunta: ¿Cuántos parámetros se necesitan para localizar con toda precisión un punto en este espacio?

Bien es sabido que sobre una recta donde se ha escogido dos puntos, O(origen) e I(1,0) todo punto, M, está perfectamente definido a partir de su abscisa x:

En un plano (P), se escogen tres puntos distintos O,I e J, y se definen los vectores:

y un punto M es localizado por su abscisa x y su ordenada y: M(x, y) significa

Si se cambia el cuerpo de los escalares, de a 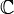, entonces el mismo punto M será deteminado por el complejo z_M =x + yi, es decir por un solo parámetro.

La dimensión de P es 1 sobre 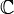y dos sobre :

Un plano real es por lo tanto una recta compleja. La apelación plano complejo para designar un plano real con escritura compleja de las coordenadas ( x + yi en vez de (x; y) ) es errónea, pero muy común.

El espacio ambiente es tridimensional y se requiere por lo tanto tres reales (x, y, z) para definir un punto. No se le puede considerar como un espacio sobre .

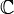En la teoría de la relatividad, se añade una cuarta variable: el tiempo, y un punto (x, y, z, t) de este espacio cuadridimensional corresponde a un evento o acontecimiento (las coordenadas nos dicen donde y cuando ocurrió).

En algunas teorías actuales, los físicos trabajan en un modelo del espacio con once dimensiones, pero sobre el conjunto de los enteros, y no los real. Como el conjunto 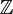de los racionales no es un cuerpo sino un anillo, el espacio no es vectorial (se dice que es un módulo). Sin embargo, la definición de la dimensión es válida en tales espacios. En este ejemplo, la mayoría de las dimensiones son enrolladas sobre sí mismas, como una serpiente que se muerde la cola. Su curvatura es enorme, pues su radio es microscópico, menor que el de un núcleo. Los espacios vectoriales no tienen curvatura.

Dimensión de un subespacio

La definición sigue siendo la misma en el caso de un subespacio, pero existe un método particular de calcularla cuando el subespacio es definido como espacio generado por sistema de vectores. Veámoslo en un ejemplo. En el espacio 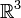, sean los vectores:

Cuatro vectores no pueden ser independientes en 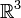, por lo tanto tienen que existir relaciones de dependencia:

lo que se puede escribir en forma matricial :

Llamemos A a la matriz anterior, y X el vector columna. Esta relación significa que el vector X pertenece al núcleo de A, que se nota Ker A (del alemán Kern, núcleo). El espacio generado es el conjunto de los

,

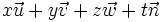es decir de los A·X: es la imagen de A.

Resulta intuitivo que cuanto mayor es el núcleo, menor es la imagen, en términos de dimensiones. Concretamente, si llamamos rango de A a la dimensión de su imagen: rg A = dim (Im A), tenemos la relación:

rg A + dim (Ker A) = dim E (E: espacio de entrada de A, aquí E = ).

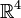Busquemos dim (Ker A):

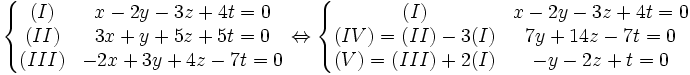
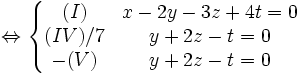
Quedan dos ecuaciones no proporcionales, por lo tanto independientes, y cada una resta 1 a la dimensión, que vale inicialmente 4. Resulta que dim (Ker A ) = 2. Se puede constatarlo de otra manera: Las dos ecuaciones permiten expresar y,luego x en función de z y t, por consiguiente solo quedan dos variables libres, y la dimensión es 2.

Aplicando la fórmula : rg A = 4 - 2 = 2. El subespacio es un plano.

Fórmula de las dimensiones de Grassmann

Si U₁ y U₂ son subespacios de un espacio vectorial de dimensión finita, se cumple:

dimU1 + dimU2 = dim(U1+U2) + dim(U1∩U2)