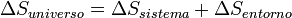Entropía (termodinámica)

Entropía (termodinámica)

Entropía (termodinámica)

La entropía describe lo irreversible de los sistemas termodinámicos. En termodinámica, la entropía (simbolizada como S) es la magnitud física que mide la parte de la energía que no puede utilizarse para producir trabajo. Es una función de estado de carácter extensivo y su valor, en un sistema aislado, crece en el transcurso de un proceso que se dé de forma natural. La palabra entropía procede del griego (ἐντροπία) y significa evolución o transformación. Fue Rudolf Clausius quien le dio nombre y la desarrolló durante la década de 1850.[1] [2]

Contenido

Evidencias

Cuando se plantea la pregunta: ¿por qué ocurren los sucesos de la manera que ocurren, y no al revés? se busca una respuesta que indique cuál es el sentido de los sucesos en la naturaleza. Por ejemplo, si se ponen en contacto dos trozos de metal con distinta temperatura, se anticipa que finalmente el trozo caliente se enfriará, y el trozo frío se calentará, logrando al final una temperatura uniforme. Sin embargo, el proceso inverso, el trozo caliente calentándose y el trozo frío enfriándose, es muy improbable a pesar de conservar la energía. El universo tiende a distribuir la energía uniformemente; es decir, a maximizar la entropía.

La función termodinámica entropía es central para la segunda Ley de la Termodinámica. La entropía puede interpretarse como una medida de la distribución aleatoria de un sistema. Se dice que un sistema altamente distribuido al azar tiene alta entropía. Puesto que un sistema en una condición improbable tendrá una tendencia natural a reorganizarse a una condición más probable (similar a una distribución al azar), esta reorganización resultará en un aumento de la entropía. La entropía alcanzará un máximo cuando el sistema se acerque al equilibrio, alcanzándose la configuración de mayor probabilidad.

La entropía, coloquialmente, puede considerarse como el desorden de un sistema, es decir, cuán homogéneo está el sistema. Un ejemplo doméstico, sería el de lanzar un vaso de cristal al suelo, este tenderá a romperse y esparcirse mientras que jamás conseguiremos que lanzando trozos de cristal se forme un vaso.

Otro ejemplo domestico: Tenemos dos envases de un litro de capacidad que contienen, respectivamente, pintura blanca y pintura negra. Con una cucharita, tomamos pintura blanca, la vertemos en el recipiente de pintura negra y mezclamos. Luego tomamos con la misma cucharita pintura negra, la vertemos en el recipiente de pintura blanca y mezclamos. Repetimos el proceso hasta que tenemos dos litros de pintura gris, que no podremos reconvertir en un litro de pintura blanca y otro de pintura negra. La entropia del conjunto ha ido en aumento hasta llegar a un máximo cuando los colores de ambos recipientes son sensiblemente iguales (sistema homogéneo).

La variación de entropía nos muestra la variación del orden molecular ocurrido en una reacción química. Si el incremento de entropía es positivo, los productos presentan un mayor desorden molecular (mayor entropía) que los reactivos. En cambio, cuando el incremento es negativo, los productos son más ordenados. Hay una relación entre la entropía y la espontaneidad de una reacción química, que viene dada por la energía de Gibbs.

Ecuaciones

Esta idea de desorden termodinámico fue plasmada mediante una función ideada por Rudolf Clausius a partir de un proceso cíclico reversible. En todo proceso reversible la integral curvilínea de 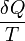\frac{\delta Q}{T} sólo depende de los estados inicial y final, con independencia del camino seguido (δQ es la cantidad de calor absorbida en el proceso en cuestión y T es la temperatura absoluta). Por tanto ha de existir una f(x) del estado del sistema, S=f(P,V,T), denominada entropía, cuya variación en un proceso reversible entre los estados 1 y 2 es: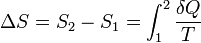

\Delta S = S_2 - S_1 = \int_1^2 \frac {\delta Q} {T}

Téngase en cuenta que como el calor no es una función de estado se usa δQ en lugar de dQ.

La entropía física, en su forma clásica, está definida por la ecuación

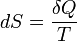
dS = \frac{\delta Q}{T}

o más simplemente, cuando no se produce variación de temperatura (proceso isotérmico):

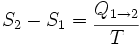
S_2 - S_1 = \begin{matrix} \cfrac{Q_{1 \to 2}}{T} \end{matrix}

donde S es la entropía, 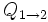Q_{1 \to 2} la cantidad de calor intercambiado entre el sistema y el entorno y T la temperatura absoluta en kelvin). Los números 1 y 2 se refieren a los estados iniciales y finales de un sistema termodinámico.

El significado de esta ecuación es el siguiente:

Cuando un sistema termodinámico pasa, en un proceso reversible e isotérmico, del estado 1 al estado 2, el cambio en su entropía es igual a la cantidad de calor intercambiado entre el sistema y el medio dividido por su temperatura absoluta.

De acuerdo con la ecuación, si el calor se transfiere al sistema, también lo hará el grado de entropía. Si la temperatura aumenta, la entropía disminuye. Y viceversa.

Las unidades de la entropía, en el Sistema Internacional, son el J/K (o Clausius) definido como la variación de entropía que experimenta un sistema cuando absorbe el calor de 1 Julio (unidad) a la temperatura de 1 Kelvin.

Cuando el sistema evoluciona irreversiblemente, la ecuación de Clausius se convierte en una inecuación:

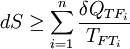
dS \ge \sum_{i=1}^n \frac{\delta Q_{TF_i}}{T_{FT_i}}

Siendo el sumatorio de las i fuentes de calor de las que recibe o transfiere calor el sistema y la temperatura de las fuentes. No obstante, sumando un término positivo al segundo miembro, podemos transformar de nuevo la expresión en una ecuación:

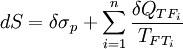
dS = {\delta \sigma}_p + \sum_{i=1}^n \frac{\delta Q_{TF_i}}{T_{FT_i}}

Al termino σp, siempre positivo, se le denomina producción de entropía y es nulo cuando el proceso es reversible salvo irreversibilidades fruto de transferencias de calor con fuentes externas al sistema. En el caso de darse un proceso reversible y adiabático, según la ecuación, dS=0, es decir, el valor de la Entropía es constante y además constituye un proceso isoentrópico.

Cero absoluto

Sólo se pueden calcular variaciones de entropía. Para calcular la entropía de un sistema es necesario fijar la entropía del mismo en un estado determinado. La Tercera ley de la termodinámica fija un estado estándar: para sistemas químicamente puros, sin defectos estructurales en la red cristalina, de densidad finita, la entropía es nula en el cero absoluto (0 K).

Esta magnitud permite definir la Segunda ley de la termodinámica, de la cual se deduce que un proceso tiende a darse de forma espontánea en un cierto sentido solamente. Por ejemplo: un vaso de agua no empieza a hervir por un extremo y a congelarse por el otro de forma espontánea, aun cuando siga cumpliéndose la condición de conservación de la energía del sistema (Primera ley de la termodinámica).

Entropía y reversibilidad

La entropía global del sistema es la entropía del sistema considerado más la entropía de los alrededores. También se puede decir que la variación de entropía del universo, para un proceso dado, es igual a su variación en el sistema más la de los alrededores:

\Delta S_{universo} = \Delta S_{sistema} + \Delta S_{entorno} \,

Si se trata de un proceso reversible, ΔS (universo) es cero pues el calor que el sistema absorbe o desprende es igual al trabajo realizado. Pero esto es una situación ideal, ya que para que esto ocurra los procesos han de ser extraordinariamente lentos y esta circunstancia no se da en la naturaleza. Por ejemplo, en la expansión isotérmica (proceso isotérmico) de un gas, considerando el proceso como reversible, todo el calor absorbido del medio se transforma en trabajo y Q=W. Pero en la práctica real el trabajo es menor ya que hay pérdidas por rozamientos, por lo tanto, los procesos son irreversibles.

Para llevar al sistema, de nuevo, a su estado original hay que aplicarle un trabajo mayor que el producido por el gas, dando como resultado una transferencia de calor hacia el entorno, con un aumento de la entropía global.

Como los procesos reales son siempre irreversibles, siempre aumentará la entropía. Así como "la energía no puede crearse ni destruirse", la entropía puede crearse pero no destruirse. Podemos decir entonces que "como el Universo es un sistema aislado, su entropía crece constantemente con el tiempo". Esto marca un sentido a la evolución del mundo físico, que llamamos "Principio de evolución".

Cuando la entropía sea máxima en el universo, esto es, exista un equilibrio entre todas las temperaturas y presiones, llegará la muerte térmica del Universo (enunciado por Clausius). Toda la energía se encontrará en forma de calor y no podrán darse transformaciones energéticas.

Interpretación estadística de la entropía

En los años 1890 - 1900 el físico austríaco Ludwig Boltzmann y otros, desarrollaron las ideas de lo que hoy se conoce como mecánica estadística, teoría profundamente influenciada por el concepto de entropía.

Una de las teorías termodinámicas estadísticas (la de Maxwell-Boltzmann), establece la siguiente relación entre la entropía y la probabilidad termodinámica:

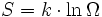
S = k \cdot \ln \Omega

Donde S es la entropía, k la constante de Boltzmann y Ω el número de microestados posibles para el sistema (ln es la función logaritmo neperiano).

La célebre ecuación se encuentra grabada sobre la lápida de la tumba de Boltzmann en el Zenmtralfriedhof de Viena, quien se suicidó en 1906, profundamente deprimido por la poca aceptación de sus teorías en el mundo académico de la época.

El significado literal de la ecuación es el siguiente:

La cantidad de entropía de un sistema es proporcional al logaritmo natural de su número de microestados posibles.

Uno de los aspectos más importantes que describe esta ecuación, es la posibilidad de dar una definición absoluta al concepto de la entropía. En la descripción clásica de la termodinámica, carece de sentido hablar del valor de la entropía de un sistema, siendo relevantes sólo los cambios en la misma. En cambio, la teoría estadística, permite definir la entropía absoluta de un sistema.

Relación de la entropía con la Teoría de la información

Recientes estudios han podido establecer una relación entre la entropía física y la entropía de la teoría de la información gracias a la revisión de la física de los agujeros negros. Según la nueva teoría de Jacob D. Bekenstein el bit de información sería equivalente a una superficie de valor 1/4 del área de Planck. De hecho, en presencia de agujeros negros la segunda ley de la termodinámica sólo puede cumplirse si se introduce la entropía generalizada o suma de la entropía convencional (Sconv) más un factor dependiente del área total (A) de agujeros negros existente en el universo, del siguiente modo:

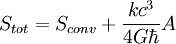
S_{tot} = S_{conv} + \frac{kc^3}{4G\hbar}A
Donde, k es la constante de Boltzmann, c es la velocidad de la luz, G es la constante de la gravitación y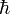 \hbar es la constante de Planck racionalizada.

Los agujeros negros almacenarían la entropía de los objetos que engulle en la superficie del horizonte de sucesos. Stephen Hawking ha tenido que ceder ante las evidencias de la nueva teoría y ha propuesto un mecanismo nuevo para la conservación de la entropía en los agujeros negros.

Simplemente, al realizar un trabajo, se ocupa muy poca energía; la entropía se encarga de medir la energía que no es usada y queda reservada en un cuerpo.

Entropía y su Relación con las Termociencias

Ya que tenemos estos conocimientos previos de lo que es la entropía debemos aplicarlos a las termociencias, supongamos que tenemos un sistema termodinámico, es decir, algo donde se propague el calor, digamos un comal para hacer tortillas de harina, cuando el calor o la energía calorífica se propaga al comal, podemos decir que el comal está calentado por completo, pero estaríamos cayendo en un error monumental debido a que nunca habrá un equilibrio térmico perfecto, porque el comal está en contacto con el aire, y el comal está calentando al aire y el aire le roba calor al comal.

En realidad si pudiéramos de alguna forma observar con unas gafas especiales este sistema enclavado o ubicado que se está llevando acabo en ese momento podríamos observar un desorden a nivel molecular o de partícula, podríamos ver u observar la partículas que componen al comal de un color encarnado mientras que las partículas del aire se van colorando a razón de que pasen por el comal.

Podremos ver también a nivel molecular un gran desorden de partículas del aire chocando unas con otras debido a la cantidad de calor que están ganando, es cuando se dice que la entropía aumenta en el sistema, alguna vez podría estar en equilibrio ese sistema, la respuesta sencillamente es no debido a que se necesitaría calentar el aire de todo el planeta para que estuviera en equilibrio con el comal, y aún en esas condiciones no estarían en equilibrio debido a que habría que calentar el sistema circundante es decir todo el sistema solar para que el sistema en realidad estuviera en equilibrio y aun así no lo estaría porque habría que calentar todo el universo y hay que recordar que el universo está en continua expansión.

Véase también

Referencias

  1. ↑ Clausius, R. (1850). «Über die bewegende Kraft der Wärme» Annalen der Physik und Chemie. Vol. 79. pp. 368-397, 500-524. Consultado el 23 de septiembre de 2009.
  2. ↑ Clausius, R. (1865). «Ueber verschiedene für die Anwendung bequeme Formen der Hauptgleichungen der mechanischen Wärmetheorie» Annalen der Physik und Chemie. Vol. 125. pp. 351-400. Consultado el 23 de septiembre de 2009.

Enlaces externos

Obtenido de "Entrop%C3%ADa (termodin%C3%A1mica)"

Wikimedia foundation. 2010.

Игры ⚽ Поможем сделать НИР

Mira otros diccionarios:

  • Entropía (termodinámica) — En Física la entropía es la magnitud termodinámica que mide la parte de la energía que no puede utilizarse para producir un trabajo. La entropía física, en su forma clásica, es definida por la ecuación dS = dQ / T …   Enciclopedia Universal

  • Entropía de formación — Saltar a navegación, búsqueda La entropía de formación de un compuesto químico (o una sustancia en estado elemental), en termodinámica y termoquímica, es la diferencia (incremento o decremento) de entropía en el proceso de su formación a partir… …   Wikipedia Español

  • Entropía — Para otros usos de este término, véase Entropía (desambiguación). Escultura dedicada a la Entropía en los jardines centrales de la Universidad de Monterrey, México En termodinámica, la entropía (simbolizada como S) es una magnitud física que… …   Wikipedia Español

  • Entropía (información) — Saltar a navegación, búsqueda Para otros usos de este término, véase Entropía. Entropía es un concepto en termodinámica, mecánica estadística y teoría de la información. Los conceptos de información y entropía están ampliamente relacionados entre …   Wikipedia Español

  • Entropia (álbum) — Saltar a navegación, búsqueda Entropia Álbum de Pain of Salvation Publicación Agosto de 1997 (Japón) Septiembre de 1999 (Europa y Sudamérica) 2000 (Estados Unidos) Grabación Primavera de 19 …   Wikipedia Español

  • entropía — (Del gr. ἐντροπία, vuelta, usado en varios sentidos figurados). 1. f. Fís. Magnitud termodinámica que mide la parte no utilizable de la energía contenida en un sistema. 2. Fís. Medida del desorden de un sistema. Una masa de una sustancia con sus… …   Diccionario de la lengua española

  • entropia — /entro pia/ s.f. [dal ted. Entropie, comp. del gr. en dentro e tropḗ rivolgimento, mutazione ]. 1. (fis.) [funzione di stato termodinamica, che può essere assunta a misura del grado di disordine di un sistema] ◀▶ sintropia. 2. (fig., non com.)… …   Enciclopedia Italiana

  • entropía — sustantivo femenino 1. Área: física Magnitud termodinámica que expresa el grado de desorden molecular de un sistema …   Diccionario Salamanca de la Lengua Española

  • Termodinámica — Sistema termodinámico típico mostrando la entrada desde una fuente de calor (caldera) a la izquierda y la salida a un disipador de calor (condensador) a la derecha. El trabajo se extrae en este caso por una serie de pistones. La termodinámica… …   Wikipedia Español

  • Entropía — (Del gr. entrope, vuelta.) ► sustantivo femenino 1 FÍSICA Magnitud termodinámica que indica el grado de desorden interno de un sistema. 2 SICOLOGÍA Medida que indica el grado de información no aprovechable de una fuente, en función del número de… …   Enciclopedia Universal

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”