Envoltura convexa

Envoltura convexa

Envoltura convexa

Envoltura convexa de un conjunto de 15 puntos en el plano

En matemática se define la envoltura convexa de un conjunto de puntos X de dimensión n como la intersección de todos los conjuntos convexos que contienen a X.[1]

Dados k puntos 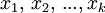x_1,\, x_2,\, ...,x_k su envoltura convexa C viene dada por la expresión: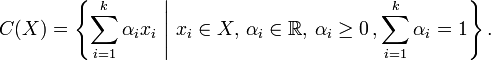

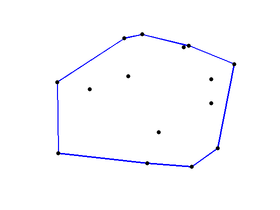
C(X) =\left\{\sum_{i=1}^k \alpha_i x_i \ \Bigg | \ x_i\in X, \, \alpha_i\in \mathbb{R}, \, \alpha_i \geq 0 \, , \sum_{i=1}^k \alpha_i=1\right\}.

En el caso particular de puntos en un plano, si no todos los puntos están alineados, entonces su envoltura convexa corresponde a un polígono convexo cuyos vértices son algunos de los puntos del conjunto inicial de puntos.

Una forma intuitiva de ver la envoltura convexa de un conjunto de puntos en el plano, es imaginar una banda elástica estirada que los encierra a todos. Cuando se libere la banda elástica tomará la forma de la envoltura convexa.

Cálculo de la envoltura convexa

En geometría computacional existen numerosos algoritmos para calcular la envoltura convexa de un conjunto finito de puntos, con diversos grados de complejidad computacional. La complejidad del algoritmo de resolución se suele estimar en función del número n de puntos de entrada, y el número h de puntos de la correspondiente envoltura convexa.

Algoritmos para el cálculo de la envoltura convexa en el plano

  • Jarvis march o gift wrapping algorithm. Propuesto por R. A. Jarvis en 1973. Es uno de los más simples y posee una complejidad computacional O(nh). En el peor de los casos su complejidad será O(n2).
  • Graham scan. Publicado en 1972, es mucho más eficiente y posee una complejidad computacional O(n log n). Si los puntos se encuentran ordenados por una de las coordenadas o por el ángulo a un vector fijo entonces la complejidad es O(n).
  • Divide and conquer. Otro algoritmo de complejidad O(n log n) publicado en 1977 por Franco P. Preparata y Hong. También es aplicable al caso tridimensional.

Referencias

  1. ↑ Mathworld
Obtenido de "Envoltura convexa"

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Combinación convexa — Dados tres puntos x1,x2,x3 en el plano como se muestra en la figura, el punto P es combinación convexa de los tres puntos, mientras que Q no lo es. (Q es sin embargo una combinación afín de …   Wikipedia Español

  • Convexidad — La convexidad de una curva o una superficie, es la zona que se asemeja al exterior de una circunferencia o una superficie esférica; es el concepto opuesto a la concavidad. Contenido 1 Conjunto convexo 1.1 Envoltura convexa de un conjunto 2… …   Wikipedia Español

  • Teorema de Gauss-Lucas — En análisis complejo, el teorema de Gauss Lucas aporta una relación geométrica entre las raíces de un polinomio P y las raíces de su derivada P . El conjunto de raíces de un polinomio real o complejo es un conjunto de puntos en el plano complejo …   Wikipedia Español

  • Criterio de Eisenstein — Saltar a navegación, búsqueda En matemática, el criterio de Eisenstein proporciona la condición suficiente para que un polinomio sea irreducible sobre Q (o, de forma equivalente, sobre Z). Si tenemos el siguiente polinomio con coeficientes… …   Wikipedia Español

  • Simplex — Saltar a navegación, búsqueda Para el algoritmo del mismo nombre, véase Algoritmo simplex. Un 3 simplejo o tetraedro que puede pensarse como una región del espacio que consiste en la parte acotada por (y que también incluye) los cuatro puntos,… …   Wikipedia Español

  • Símplex — Para el algoritmo del mismo nombre, véase Algoritmo simplex. Un 3 simplejo o tetraedro que puede pensarse como una región del espacio que consiste en la parte acotada por (y que también incluye) los cuatro puntos, los seis segmentos de línea y… …   Wikipedia Español

  • Lema de Radon — El lema de Radon, o simplemente teorema de Radon es un teorema de geometría combinatoria. Se enuncia de la siguiente manera: Si se toman d+2 puntos de Rd, se pueden repartir en dos conjuntos disjuntos A y B tales que las envolventes convexas de A …   Wikipedia Español

  • Computadora analógica — Computador analógico. Una computadora analógica u ordenador real es un tipo de computadora que utiliza dispositivos electrónicos o mecánicos para modelar el problema que resuelven utilizando un tipo de cantidad física para representar otra. Para… …   Wikipedia Español

  • Desigualdad de Shapiro — Saltar a navegación, búsqueda En matemáticas, la desigualdad de Shapiro es una desigualdad que fue descubierta por H. Shapiro y Vladímir Drínfeld. Enunciado Sea n un número natural y …   Wikipedia Español

  • Hipercubo — Teseractos Diagrama Schlegel Tipo Politopo regular Familia Hipercubo Celdas 8 (4.4.4) …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”