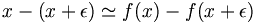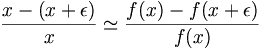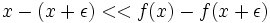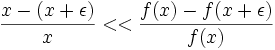En el subcampo matemático del análisis numérico, la estabilidad numérica es una propiedad de los algoritmos numéricos. Describe cómo los errores en los datos de entrada se propagan a través del algoritmo. En un método estable, los errores debidos a las aproximaciones se atenúan a medida que la computación procede. En un método inestable, cualquier error en el procesamiento se magnifica conforme el cálculo procede. Métodos inestables generan rápidamente basura y son inútiles para el procesamiento numérico.

La estabilidad numérica de un método junto con el número condición (en:condition number) define cuán buen resultado podemos obtener usando métodos aproximados para calcular cierto problema matemático.

Algunas veces un sólo cálculo puede ser logrado de varias maneras, todas las cuales son algebraicamente idénticas en términos de números ideales reales o complejos, pero en la práctica producen resultados diferentes conforme(as) tienen diferentes niveles de estabilidad numérica. Una de las tareas comunes del análisis numérico es tratar de seleccionar algoritmos robustos -- esto es, que tienen una buena estabilidad numérica en un amplio intervalo(range) de situaciones. Éstos métodos están frecuentemente disponibles para usuarios de lenguajes de programación como librerías de computación matemática ( ver mathematical computing libraries). El uso apropiado de librerías (libraries) de computación matemática es usualmente muy superior a algoritmos numéricos "roll you own".

Definición

Dado un algoritmo f(x), con x los datos de entrada y ε el error en los datos de entrada, decimos que el algoritmo es numéricamente estable, es decir que el algoritmo depende continuamente de los parámetros, para el error absoluto si

y numéricamente estable para el error relativo si

Decimos que un algoritmo es numéricamente inestable para el error absoluto si

y numéricamente inestable para el error relativo si

Notas

Cuando se calculan soluciones numéricas a ciertas ecuaciones diferenciales parciales, la estabilidad se consigue algunas veces incluyendo la difusión numérica. La difusión numérica es un término matemático que asegura que errores de redondeo y de otro tipo en los cálculos se separen(spread out) y no se sumen para causar que el cálculo se desborde "blow up".

La estabilidad numérica es la razón por la cual no se puede normalmente probar (testear) un código numérico como la simulación del clima corriéndolo hacia atrás (backward). Correr el código hacia adelante (forward) incluye métodos numéricos para asegurar que los erroes de aproximación aleatorios se vuelvan (become) menos y menos importantes mientras (as) el cálculo procede asegurando la estabilidad numérica. Correr el código hacia atrás causa que esos mecanismos magnifiquen esos errores generando resultados inútiles.

Cuando se resuleve un problema numérico con un método aproximado, dos tipos de errorres pueden ocurrir:

• Errores de truncamiento: Sólo se puede hacer un número finito de cálculos. Ejemplos: calculando una función transcendental usando su serie de Taylor, integrando usando una suma finita de rectángulos.
• Errores de redondeo: Ciertos números necesitan un infinito número de dígitos para ser representados (pi), cuando se redondean estos números los errores de redondeo se propagarán a través del cálculo.