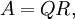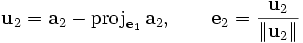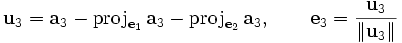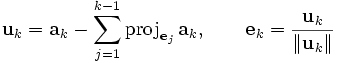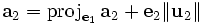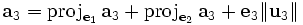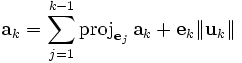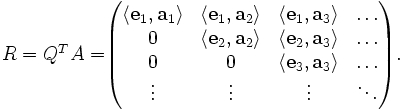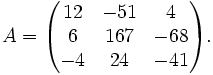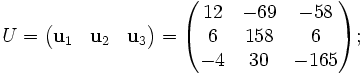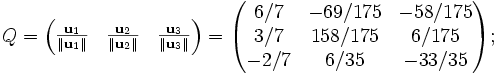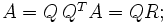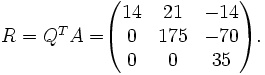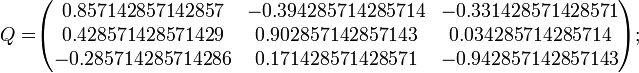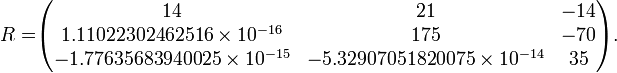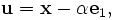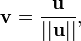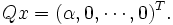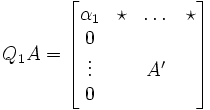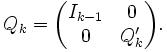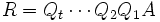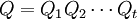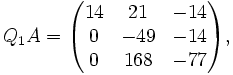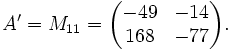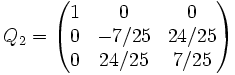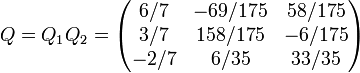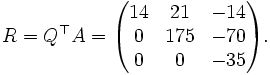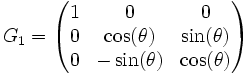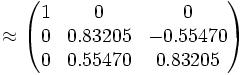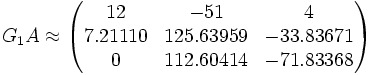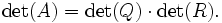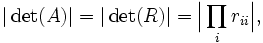Factorización QR

Saltar a navegación, búsqueda

En álgebra lineal, la descomposición o factorización QR de una matriz es una descomposición de la misma como producto de una matriz ortogonal por una triangular superior. La descomposición QR es la base del algoritmo QR utilizado para el cálculo de los vectores y valores propios de una matriz.

Definición

La descomposición QR de una matriz cuadrada real A es

$A = QR, \,$

donde Q es una matriz ortogonal (Q^TQ = I ) y R es una matriz triangular superior.

Cálculo de la descomposición QR

Mediante el método de ortogonalización de Gram-Schmidt

Recurriendo al método de ortogonalización de Gram-Schmidt, con las columnas de A como los vectores a procesar.

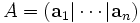$A=(\mathbf{a}_1| \cdots|\mathbf{a}_n)$ . Entonces

$\mathbf{u}_1 = \mathbf{a}_1, \qquad\mathbf{e}_1 = {\mathbf{u}_1 \over \|\mathbf{u}_1\|}$

$\mathbf{u}_2 = \mathbf{a}_2-\mathrm{proj}_{\mathbf{e}_1}\,\mathbf{a}_2, \qquad\mathbf{e}_2 = {\mathbf{u}_2 \over \|\mathbf{u}_2\|}$

$\mathbf{u}_3 = \mathbf{a}_3-\mathrm{proj}_{\mathbf{e}_1}\,\mathbf{a}_3-\mathrm{proj}_{\mathbf{e}_2}\,\mathbf{a}_3, \qquad\mathbf{e}_3 = {\mathbf{u}_3 \over \|\mathbf{u}_3\|}$

$\vdots$

$\mathbf{u}_k = \mathbf{a}_k-\sum_{j=1}^{k-1}\mathrm{proj}_{\mathbf{e}_j}\,\mathbf{a}_k,\qquad\mathbf{e}_k = {\mathbf{u}_k\over\|\mathbf{u}_k\|}$

Naturalmente, utilizamos los a_is de A para obtener:

$\mathbf{a}_1 = \mathbf{e}_1\|\mathbf{u}_1\|$

$\mathbf{a}_2 = \mathrm{proj}_{\mathbf{e}_1}\,\mathbf{a}_2+\mathbf{e}_2\|\mathbf{u}_2\|$

$\mathbf{a}_3 = \mathrm{proj}_{\mathbf{e}_1}\,\mathbf{a}_3+\mathrm{proj}_{\mathbf{e}_2}\,\mathbf{a}_3+\mathbf{e}_3\|\mathbf{u}_3\|$

$\vdots$

$\mathbf{a}_k = \sum_{j=1}^{k-1}\mathrm{proj}_{\mathbf{e}_j}\,\mathbf{a}_k+\mathbf{e}_k\|\mathbf{u}_k\|$

Ahora estas ecuaciones pueden ser escritas en forma matricial de esta manera:

$\left(\mathbf{e}_1\left|\ldots\right|\mathbf{e}_n\right) \begin{pmatrix} \|\mathbf{u}_1\| & \langle\mathbf{e}_1,\mathbf{a}_2\rangle & \langle\mathbf{e}_1,\mathbf{a}_3\rangle & \ldots \\ 0 & \|\mathbf{u}_2\| & \langle\mathbf{e}_2,\mathbf{a}_3\rangle & \ldots \\ 0 & 0 & \|\mathbf{u}_3\| & \ldots \\ \vdots & \vdots & \vdots & \ddots \end{pmatrix}$ :::::::::

El producto de cada fila con cada columa de las matrices de arriba, nos da la respectiva columna de A con la que comenzamos y, por tanto, dada la matriz A, la hemos factorizado en una matriz ortogonal Q (la matriz de e_ks), aplicando el proceso de Gram-Schmidt, y la matriz resultante triangular superior es R.

Alternativamente, la matriz $\begin{matrix} R \end{matrix}$ puede clacularse de la siguiente manera:

Recordemos que: 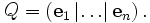$\begin{matrix}Q\end{matrix} = \left(\mathbf{e}_1\left|\ldots\right|\mathbf{e}_n\right).$ Entonces, tenemos

$\begin{matrix} R = Q^{T}A = \end{matrix} \begin{pmatrix} \langle\mathbf{e}_1,\mathbf{a}_1\rangle & \langle\mathbf{e}_1,\mathbf{a}_2\rangle & \langle\mathbf{e}_1,\mathbf{a}_3\rangle & \ldots \\ 0 & \langle\mathbf{e}_2,\mathbf{a}_2\rangle & \langle\mathbf{e}_2,\mathbf{a}_3\rangle & \ldots \\ 0 & 0 & \langle\mathbf{e}_3,\mathbf{a}_3\rangle & \ldots \\ \vdots & \vdots & \vdots & \ddots \end{pmatrix}.$

Note que $\langle\mathbf{e}_j,\mathbf{a}_j\rangle = \|\mathbf{u}_j\|,$ $\langle\mathbf{e}_j,\mathbf{a}_k\rangle = 0 \mathrm{~~for~~} j > k,$ and $Q Q T = I$ , so $Q T = Q - 1$ .

Ejemplo

Si se considera la descomposición de

$A = \begin{pmatrix} 12 & -51 & 4 \\ 6 & 167 & -68 \\ -4 & 24 & -41 \end{pmatrix} .$

Se busca la matriz ortogonal $Q$ tal que

$\begin{matrix} Q\,Q^{T} = I. \end{matrix}$

Por lo que calculamos $Q$ mediante Gram-Schmidt como sigue:

$U = \begin{pmatrix} \mathbf u_1 & \mathbf u_2 & \mathbf u_3 \end{pmatrix} = \begin{pmatrix} 12 & -69 & -58 \\ 6 & 158 & 6 \\ -4 & 30 & -165 \end{pmatrix};$

$Q = \begin{pmatrix} \frac{\mathbf u_1}{\|\mathbf u_1\|} & \frac{\mathbf u_2}{\|\mathbf u_2\|} & \frac{\mathbf u_3}{\|\mathbf u_3\|} \end{pmatrix} = \begin{pmatrix} 6/7 & -69/175 & -58/175 \\ 3/7 & 158/175 & 6/175 \\ -2/7 & 6/35 & -33/35 \end{pmatrix};$

Por lo tanto, tenemos

$\begin{matrix} A = Q\,Q^{T}A = Q R; \end{matrix}$

$\begin{matrix} R = Q^{T}A = \end{matrix} \begin{pmatrix} 14 & 21 & -14 \\ 0 & 175 & -70 \\ 0 & 0 & 35 \end{pmatrix}.$

Considerando errores numéricos de operar con precisión finita en MATLAB, tenemos que

$\begin{matrix} Q = \end{matrix} \begin{pmatrix} 0.857142857142857 & -0.394285714285714 & -0.331428571428571 \\ 0.428571428571429 & 0.902857142857143 & 0.034285714285714 \\ -0.285714285714286 & 0.171428571428571 & -0.942857142857143 \end{pmatrix};$

$\begin{matrix} R = \end{matrix} \begin{pmatrix} 14 & 21 & -14 \\ 1.11022302462516 \times 10^{-16} & 175 & -70 \\ -1.77635683940025 \times 10^{-15} & -5.32907051820075 \times 10^{-14} & 35 \end{pmatrix}.$

Mediante el uso de reflexiones de Householder

Una transformación de Householder o reflexión de Householfer es una transformación que refleja el espacio con respecto a un plano determinado. Esta propiedad se puede utilizar para realizar la transformación QR de una matriz si tenemos en cuenta que es posible elegir la matriz de Householder de manera que un vector elegido quede con una única componente no nula tras ser transformado (es decir, premultiplicando por la matriz de Householder). Gráficamente, esto significa que es posible reflejar el vector elegido respecto de un plano de forma que el reflejo quede sobre uno de los ejes de la base cartesiana.

La manera de elegir el plano de reflexión y formar la matiz de Householder asociada es el siguiente:

Sea 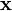$\mathbf{x}$ un vector columna arbitrario m-dimensional tal que || 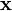$\mathbf{x}$ || = |α|, donde α es un escalar; (si el algoritmo se implementa utilizando aritmética de coma flotante, entonces α debe adoptar el signo contrario que $x$ ₁ para evitar pérdida de precisión).

Entonces, siendo 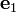$\mathbf{e}_1$ el vector (1,0,...,0)^T, y ||·|| la norma euclídea, se define:

$\mathbf{u} = \mathbf{x} - \alpha\mathbf{e}_1,$

$\mathbf{v} = {\mathbf{u} \over ||\mathbf{u}||},$

$Q = I - 2 \mathbf{v}\mathbf{v}^T.$

$v$ es un vector unitario perpendicular al plano de reflexión elegido. $Q$ es una matriz de Householder asociada a dicho plano.

$Qx = (\alpha, 0, \cdots, 0)^T.\,$

Esta propiedad se puede usar para transformar gradualmente los vectores columna de una matriz A de dimensiones m por n en una matriz triangular superior. En primer lugar se multiplica A con la matriz de Householder Q₁ que obtenemos al elegir como vector 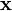$\mathbf{x}$ la primera columna de la matriz. Esto proporciona una matriz QA con ceros en la primera columna (excepto el elemento de la primera fila).

$Q_1A = \begin{bmatrix} \alpha_1&\star&\dots&\star\\ 0 & & & \\ \vdots & & A' & \\ 0 & & & \end{bmatrix}$

el procedimiento se puede repetir para A′ (que se obtiene de A eliminando la primera fila y columna), obteniendo así una matriz de Householder Q′₂. Hay que tener en cuenta que Q′₂ es menor que Q₁. Para conseguir que esta matriz opere con Q₁A en lugar de A′ es necesario expandirla hacia arriba a la izquierda, completando con un uno en la diagonal, o en general:

$Q_k = \begin{pmatrix} I_{k-1} & 0\\ 0 & Q_k'\end{pmatrix}.$

Tras repetir el proceso $t$ veces, donde $t = min(m - 1, n)$ ,

$R = Q_t \cdots Q_2Q_1A$

es una matriz triangular superior. De forma que tomando

$Q = Q_1Q_2 \cdots Q_t$

$A = Q R$ es una descomposición QR de la matriz $A$ .

Este método tiene una estabilidad numérica mayor que la del método de Gram-Schmidt descrito arriba.

Una pequeña variación de este método se utiliza para obtener matrices semejentes con forma de Hessenberg, muy útiles en el cálculo de autovalores por acelerar la convergencia del algoritmo QR reduciendo así enormemente su coste computacional.

Ejemplo

Vamos a calcular la descomposición de la matriz

$A = \begin{pmatrix} 12 & -51 & 4 \\ 6 & 167 & -68 \\ -4 & 24 & -41 \end{pmatrix}.$

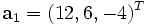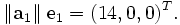
En primer lugar necesitamos encontrar una reflexión que transforme la primera columna de la matriz A, vector $\mathbf{a}_1 = (12, 6, -4)^T$ , en $\|\mathbf{a}_1\| \;\mathrm{e}_1 = (14, 0, 0)^T.$

usando la expresión,

$\mathbf{u} = \mathbf{x} - \alpha\mathbf{e}_1,$

$\mathbf{v} = {\mathbf{u} \over |\mathbf{u} |},$

en nuestro caso :

α = 14

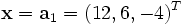
y $\mathbf{x} = \mathbf{a}_1 = (12, 6, -4)^T$

Por lo tanto

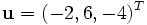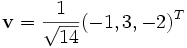$\mathbf{u} = (-2, 6, -4)^T$ y $\mathbf{v} = {1 \over \sqrt{14}}(-1, 3, -2)^T$ , entonces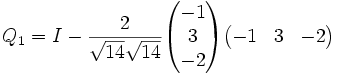

$Q_1 = I - {2 \over \sqrt{14}\sqrt{14}} \begin{pmatrix} -1 \\ 3 \\ -2 \end{pmatrix}\begin{pmatrix} -1 & 3 & -2 \end{pmatrix}$

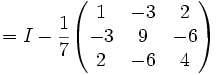
$= I - {1 \over 7}\begin{pmatrix} 1 & -3 & 2 \\ -3 & 9 & -6 \\ 2 & -6 & 4 \end{pmatrix}$

$= \begin{pmatrix} 6/7 & 3/7 & -2/7 \\ 3/7 &-2/7 & 6/7 \\ -2/7 & 6/7 & 3/7 \\ \end{pmatrix}.$

Ahora observamos:

$Q_1A = \begin{pmatrix} 14 & 21 & -14 \\ 0 & -49 & -14 \\ 0 & 168 & -77 \end{pmatrix},$

con lo que ya casi tenemos una matriz triangular. Sólo necesitamos hacer cero en el elemento (3,2).

Tomando la submatriz bajo el (1, 1) y aplicando de nuevo el proceso a

$A' = M_{11} = \begin{pmatrix} -49 & -14 \\ 168 & -77 \end{pmatrix}.$

Mediante el mismo método que antes obtenemos la matriz de Householder

$Q_2 = \begin{pmatrix} 1 & 0 & 0 \\ 0 & -7/25 & 24/25 \\ 0 & 24/25 & 7/25 \end{pmatrix}$

Finalmente obtenemos

$Q=Q_1Q_2=\begin{pmatrix} 6/7 & -69/175 & 58/175\\ 3/7 & 158/175 & -6/175 \\ -2/7 & 6/35 & 33/35 \end{pmatrix}$

$R=Q^\top A=\begin{pmatrix} 14 & 21 & -14 \\ 0 & 175 & -70 \\ 0 & 0 & -35 \end{pmatrix}.$

La matriz Q es ortogonal y R es triangular superior, de forma que A = QR es la descomposición QR buscada.

Mediante rotaciones de Givens

Las descomposiciones QR también puden calcularse utilizando una serie de rotaciones de Givens. Cada rotación anula (hace cero) un elemento en la subdiagonal de la matriz, formando de este modo la matriz R. La concatenación de todas las rotaciones de Givens realizadas, forma la matriz ortogonal Q.

En la práctica, las rotaciones de Givens no se utilizan en la actualidad para construir una matriz completa y realizar un producto de matrices. En su lugar, se utiliza un procedimiento de rotación de Givens, que es equivalente a la multiplicación reducida de matrices de Givens, sin el trabajo extra de manejar los elementos reducidos. El procedimiento de rotación de Givens es útil en situaciones donde sólo pocos elementos fuera de la diagonal necesitan ser anulados y es más facil de paralelizar que las transformaciones de Householder.

Ejemplo

Calculemos la descomposición de

$A = \begin{pmatrix} 12 & -51 & 4 \\ 6 & 167 & -68 \\ -4 & 24 & -41 \end{pmatrix}$

Primero, necesitamos formar una matriz de rotación tal que hagamos cero el elemento más inferior a la izquierda, 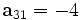$\mathbf{a}_{31} = -4$ . Construimos esta matriz empleando el método de la rotación de Givens y llamamos la matriz resultante $G 1$ . Rotamos primero el vector $(6, - 4)$ , representándolo a lo largo del eje X. Este vector forma un ángulo 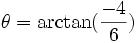$\theta = \arctan({-4 \over 6})$ . Creamos la matriz ortogonal de rotación de Givens, $G 1$ :

$G_1 = \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos(\theta) & \sin(\theta) \\ 0 & -\sin(\theta) & \cos(\theta) \end{pmatrix}$

$\approx \begin{pmatrix} 1 & 0 & 0 \\ 0 & 0.83205 & -0.55470 \\ 0 & 0.55470 & 0.83205 \end{pmatrix}$

Y el resultado de $G 1 A$ tiene ahora un cero en el 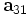$\mathbf{a}_{31}$ elemento.

$G_1A \approx \begin{pmatrix} 12 & -51 & 4 \\ 7.21110 & 125.63959 & -33.83671 \\ 0 & 112.60414 & -71.83368 \end{pmatrix}$

Procedemos análogamente con las matrices de Givens $G 2$ y $G 3$ , que hacen cero los elementos subdiagonales $a 21$ y $a 32$ , formando una matriz rectangular $R$ . La matriz ortogonal $Q T$ es formada a partir del producto en cadena de todas las matrices de Givens $Q T = G 3 G 2 G 1$ . Luego tenemos $G 3 G 2 G 1 A = Q T A = R$ , y la descomposición QR es $A = Q R$ .

Relación con el determinante

Es posible utilizar la descomposición QR para encontrar el valor absoluto del determinante de una matriz. Suponiendo que una matriz se descompone según $A = Q R$ . Entonces se tiene

$\det(A)=\det(Q)\cdot\det(R).$

Puesto que Q es unitaria, $| det(Q) | = 1$ . Por tanto,

$|\det(A)|=|\det(R)|=\Big|\prod_{i} r_{ii}\Big|,$

donde $r i i$ son los valores de la diagonal de R.

Obtenido de "Factorizaci%C3%B3n QR"

Categorías: Matrices | Álgebra lineal numérica

Wikimedia foundation. 2010.

Игры ⚽ Поможем написать реферат

Mira otros diccionarios:

Factorización — Saltar a navegación, búsqueda En álgebra, la factorización es expresar un objeto o número (por ejemplo, un número compuesto, una matriz o un polinomio) como producto de otros objetos más pequeños (factores), (en el caso de números debemos… … Wikipedia Español
Factorización LU — Saltar a navegación, búsqueda En el álgebra lineal, la factorización o descomposición LU es una forma de factorización de una matriz como el producto de una matriz triangular inferior y una superior. Debido a la inestabilidad de éste método, por… … Wikipedia Español
Factorización — En matemáticas, factorización es la descomposición de un objeto en una lista de objetos más pequeños (factores), que al multiplicarlos todos resulta el objeto original. Por ejemplo, el número 15 se factoriza en números primos 3 × 5; y el… … Enciclopedia Universal
Factorización de matrices — Saltar a navegación, búsqueda En álgebra lineal la factorización de una matriz es la descomposición de la misma como producto de dos o más matrices según una forma canónica. Según las aplicaciones de la factorización podemos distinguir los… … Wikipedia Español
Factorización de enteros — Saltar a navegación, búsqueda En teoría de números, el problema de la factorización de enteros consiste en encontrar un divisor no trivial de un número compuesto; Por ejemplo dado el número 91, el reto es encontrar un número tal como el 7 que lo… … Wikipedia Español
Factorización de Cholesky — Saltar a navegación, búsqueda En matemáticas, la factorización o descomposición de Cholesky toma su nombre del matemático André Louis Cholesky, quien encontró que una matriz simétrica definida positiva puede ser descompuesta como el producto de… … Wikipedia Español
Factorización de rango — Saltar a navegación, búsqueda Dada una matriz A, de dimensiones y de rango r, una descomposición de rango de A es un producto A = CF, donde C es una matriz y F es una matriz … Wikipedia Español
Factorización de Schur — Saltar a navegación, búsqueda En álgebra lineal, la descomposición de Schur o triangulación de Schur es una importante descomposición matricial. Definición Si A es una matriz cuadrada sobre números complejos, entonces A puede descomponerse como… … Wikipedia Español
Método de factorización de Euler — El método de factorización de Euler es un método de factorización basado en la representación de un entero positivo N como la suma de dos cuadrados de dos maneras distintas: N = a2 + b2 = c2 + d2 Aunque la factorización algebraica de números… … Wikipedia Español
Teorema de factorización de Weierstrass — En matemática, concretamente en análisis complejo, el teorema de factorización de Weierstrass, llamado así en honor a Karl Weierstrass, asegura que las funciones enteras pueden ser representadas mediante un producto que envuelve sus ceros. Además … Wikipedia Español

Los diccionarios y las enciclopedias sobre el Académico

Factorización QR

Factorización QR

Contenido

Definición

Cálculo de la descomposición QR

Mediante el método de ortogonalización de Gram-Schmidt

Ejemplo

Mediante el uso de reflexiones de Householder

Ejemplo

Mediante rotaciones de Givens

Ejemplo

Relación con el determinante

Mira otros diccionarios:

Compartir el artículo y extractos

Los diccionarios y las enciclopedias sobre el Académico

Wikipedia Español

Factorización QR

Factorización QR

Contenido

Definición

Cálculo de la descomposición QR

Mediante el método de ortogonalización de Gram-Schmidt

Ejemplo

Mediante el uso de reflexiones de Householder

Ejemplo

Mediante rotaciones de Givens

Ejemplo

Relación con el determinante

Mira otros diccionarios:

Compartir el artículo y extractos

Link directo