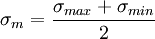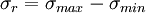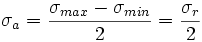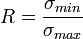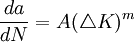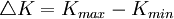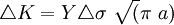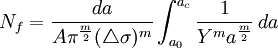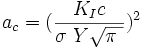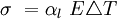Fatiga de materiales

Fatiga de materiales

Fatiga de materiales

En ingeniería y, en especial, en ciencia de materiales, la fatiga de materiales se refiere a un fenómeno por el cual la rotura de los materiales bajo cargas dinámicas cíclicas (fuerzas repetidas aplicadas sobre el material) se produce ante cargas inferiores a las cargas estáticas que producirían la rotura. Un ejemplo de ello se tiene en un alambre: flexionándolo repetidamente se rompe con facilidad, pero la fuerza que hay que hacer para romperlo en una sóla flexión es muy grande. La fatiga es una forma de rotura que ocurre en estructuras sometidas a tensiones dinámicas y fluctuantes (puentes, automóviles, aviones, etc.). Su principal peligro es que puede ocurrir a una tensión menor que la resistencia a tracción o el límite elástico para una carga estática, y aparecer sin previo aviso, causando roturas catastróficas. Es un fenómeno muy importante, ya que es la primera causa de rotura de los materiales metálicos (aproximadamente el 90%), aunque también está presente en polímeros (plásticos, composites,...), y en cerámicas.

La rotura por fatiga tiene aspecto frágil aún en metales dúctiles, puesto que no hay apenas deformación plástica asociada a la rotura. El proceso consiste en un inicio y posterior propagación de fisuras, que crecen desde un tamaño incial microscópico hasta un tamaño macroscópico capaz de comprometer la integridad estructural del material. La superficie de fractura es perpendicular a la dirección del esfuerzo. Aunque es un fenómeno que, sin definición formal, era reconocido desde antiguo, este comportamiento no fue de interés real hasta la Revolución Industrial, cuando, a mediados del siglo XIX comenzaron a producirse roturas en los ejes de las ruedas de los trenes, que pugnaban, por aquel entonces, por imponerse como medio de locomoción.

Contenido

Teorías sobre la fatiga

Para explicar el fenómeno se propusieron teorías que justificaban la pérdida de resistencia mecánica en la alteración de la estructura interna del acero por campos magnéticos o por el propio giro del eje. Por absurdas que puedan parecer estas teorías, hay que tener en cuenta que por entonces los conocimientos relativos a la estructura interna de los materiales eran muy limitados, aunque se sabía que el proceso de fabricación condicionaba la textura del material confiriéndole unas determinadas propiedades.

No es extraño entonces que se razonara que la rotura inesperada se produjera por la transformación de la estructura «fibrosa» del acero en una estructura «cristalina», sin que los mismos que defendían estas teorías supieran muy bien a qué se referían.

Hacia 1845, Rankine demostró que la reducción de las concentraciones de tensiones alargaba la vida del eje. Posteriormente, hacia 1860, Wöhler desarrolló diversas máquinas de ensayo para el estudio sistemático del fenómeno, una de las cuales, la probeta rotatoria, inspira los actuales ensayos de fatiga de materiales férricos.

Wöhler extrajo dos conclusiones de aquellos ensayos: la primera, que las fuerzas necesarias para provocar la rotura con cargas dinámicas son muy inferiores a las necesarias en el caso estático, y la segunda, que existe un umbral por debajo del cual las probetas no se rompían (límite de fatiga).

Ya en el siglo XX, Humfrey y Ewing observaron que, bajo cargas dinámicas, aparecían deformaciones por deslizamiento similares a las obtenidas en el caso estático, de modo que el progreso de dichas líneas era el que conducía a la rotura. Posteriormente, Hanson y Gough introdujeron la hipótesis del endurecimiento por deformación (acritud) para explicar la existencia del límite de fatiga, de modo que con cargas pequeñas el endurecimiento llegaba a compensar y detener el avance del deslizamiento.

Actualmente, aunque se acepta la teoría del endurecimiento/deslizamiento, no existe una formulación cuantitativa que permita realizar un cálculo fiable. No obstante, la multitud de datos disponibles, especialmente para materiales férricos y otros materiales metálicos, ha permitido desarrollar métodos de cálculo para el diseño de piezas confiables. Este no es el caso de materiales de aparición reciente, para los que es necesaria la fabricación y el ensayo de prototipos.

Tensiones cíclicas

Ejemplo de onda senoidal. En este caso hay que imaginar que la tensión representada es una tensión con ciclos de tracción (cuando es positiva) y de compresión (cuando es negativa).

La tensión puede ser axial (tensión y compresión), de flexión o torsional. En general, son posibles tres modos distintos de tensión fluctuante en el tiempo:

  1. Representado esquemáticamente por una onda senoidal del tiempo, en la que la amplitud es simétrica y varía de un valor máximo a un mínimo igual a la tensión aplicada. Se denomina ciclo de carga invertida.
  2. Denominado ciclo de carga repetida, los máximos y mínimos son asimétricos con respecto al nivel cero de carga.
  3. Aleatorio: el nivel de tensión puede variar al azar en amplitud y frecuencia.

La amplitud de la tensión varía alrededor de un valor medio, el promedio de las tensiones máxima y mínima en cada ciclo:

\sigma_{m} = \frac {\sigma_{max} + \sigma_{min}}{2}

El intervalo de tensiones es la diferencia entre tensión máxima y mínima

\sigma_{r} = \sigma_{max} - \sigma_{min} \

La amplitud de tensión es la mitad del intervalo de tensiones

\sigma_{a} = \frac {\sigma_{max} - \sigma_{min}}{2} = \frac {\sigma_{r}} {2}

El cociente de tensiones R es el cociente entre las amplitudes mínima y máxima

R = \frac {\sigma_{min}}{\sigma_{max}}

Por convención, los esfuerzos a tracción son positivos y los de compresión son negativos. Para el caso de un ciclo con inversión completa de carga, el valor de R es igual a -1.

Curva S-N

Curva S-N representativa.

Estas curvas se obtienen a través de una serie de ensayos donde una probeta del material se somete a tensiones cíclicas con una amplitud máxima relativamente grande (aproximadamente 2/3 de la resistencia estática a tracción). Se cuentan los ciclos hasta rotura. Este procedimiento se repite en otras probetas a amplitudes máximas decrecientes.

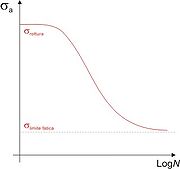
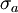Los resultados se representan en un diagrama de tensión, S, frente al logaritmo del número N de ciclos hasta la rotura para cada una de las probetas. Los valores de S se toman normalmente como amplitudes de la tensión \sigma_{a} \ .

Se pueden obtener dos tipos de curvas S-N. A mayor tensión, menor número de ciclos hasta rotura. En algunas aleaciones férreas y en aleaciones de titanio, la curva S-N se hace horizontal para valores grandes de N, es decir, existe una tensión límite, denominada límite de fatiga, por debajo del cual la rotura por fatiga no ocurrirá.

Curva S-N de un Aluminio frágil, se puede observar cómo la curva decrece y tiende a decrecer hasta llegar a rotura.

Suele decirse, de manera muy superficial, que muchas de las aleaciones no férreas (aluminio, cobre, magnesio, etc.) no tienen un límite de fatiga, dado que la curva S-N continúa decreciendo al aumentar N. Según esto, la rotura por fatiga ocurrirá independientemente de la magnitud de la tensión máxima aplicada, y por tanto, para estos materiales, la respuesta a fatiga se especificaría mediante la resistencia a la fatiga que se define como el nivel de tensión que produce la rotura después de un determinado número de ciclos. Sin embargo, esto no es exacto: es ingenuo creer que un material se romperá al cabo de tantos ciclos, no importa cúan ridículamente pequeña sea la tensión presente.

En rigor, todo material cristalino (metales,...) presenta un límite de fatiga. Ocurre que para materiales como la mayoría de los férricos, dicho límite suele situarse en el entorno del millón de ciclos (para ensayos de probeta rotatoria), para tensiones internas que rondan 0,7-0,45 veces el límite elástico del material; mientras que para aquellos que se dicen sin límite de fatiga, como el aluminio, se da incluso para tensiones muy bajas (en el alumnio, de 0,1-0,2 veces dicho límite), y aparece a ciclos muy elevados (en el aluminio puede alcanzar los mil millones de ciclos; en el titanio pueden ser, según aleaciones, cien millones de ciclos o incluso, excepcionalmente un billón de ciclos). Como en general no se diseñan máquinas ni elementos de manera que las máximas tensiones sean de 0,1-0,2 veces el límite elástico del material, pues en ese caso se estarían desaprovechando buena parte de las capacidades mecánicas del material, y como tampoco se suele diseñar asumiendo valores de vida por encima del millón de ciclos, en la práctica este tipo de materiales no van a poder presentar su límite de fatiga, aunque sí lo tienen.

Esta confusión surge de la propia naturaleza de las curvas S-N de Wöhler, que fueron concebidas en el siglo XIX para los aceros. Al ampliarse el tipo de materiales metálicos usuales en ingeniería, los mismos conceptos y las mismas curvas se trasladaron a otros metales cuyo comportamiento a fatiga es esencialmente diferente (de hecho, es una característica propia de la fatiga la gran variabilidad de comportamientos que presenta en los distintos tipos de materiales). Y como quiera que el acero ha sido y es la piedra angular de la ingeniería, interesaba comparar las propiedades de los demás metales con respecto al mismo: es y era común que, al ensayar materiales, los ensayos se suspendieran una vez superado el millón de ciclos, considerando que no interesaba caracterizar materiales por encima de ese límite temporal.

Resistencia a la fatiga para diversos materiales.

Otro parámetro importante que caracteriza el comportamiento a fatiga de un material es la vida a fatiga Nf. Es el número de ciclos para producir una rotura a un nivel especificado de tensiones.

Además, el conocimiento del comportamiento a fatiga no es igual en todos los materiales: el material mejor conocido, más ensayado y más fiable en cuanto a predicciones a fatiga es la familia de los aceros. De otros materiales metálicos de uso común como el aluminio, el titanio, aleaciones de cobre, níquel, magnesio o cromo, se dispone de menos información (decreciente ésta con la novedad de la aleación), aunque la forma de los criterios de cálculo a fatiga y de las curvas S-N parece regular, y es parecida a la de los de los aceros, y se considera que su fiabilidad es alta. Para materiales cerámicos, por el contrario, se dispone de muy poca información, y de hecho, el estudio de la fatiga en ellos y en polímeros y materiales compuestos es un tema de candente investigación actual.

En todo caso, existe una diferencia notable entre la teoría y la realidad. Esto conduce a incertidumbres significativas en el diseño cuando la vida a fatiga o el límite de fatiga son considerados. La dispersión en los resultados es una consecuencia de la sensibilidad de la fatiga a varios parámetros del ensayo y del material que son imposibles de controlar de forma precisa. Estos parámetros incluyen la fabricación de las probetas y la preparación de las superficies, variables metalúrgicas, alineamiento de la probeta en el equipo de ensayos, tensión media y frecuencia de carga del ensayo.

Aproximadamente la mitad de las probetas ensayadas se rompen a niveles de tensión que están cerca del 25% por debajo de la curva. Esto suele asociarse a la presencia de fuentes de concentración de tensiones internas, tales como defectos, impurezas, entallas, ralladuras,..., que han permanecido indetectadas.

Se han desarrollado técnicas estadísticas y se han utilizado para manejar este fallo en términos de probabilidades. Una manera adecuada de presentar los resultados tratados de esta manera es con una serie de curvas de probabilidad constante.

Fatiga de bajo número de ciclos (oligofatiga) < 103 − 105 ciclos.

Fatiga de alto número de ciclos > 103 − 105 ciclos.

Inicio y propagación de la grieta

Muestra animada de una rotura por fatiga.

El proceso de rotura por fatiga se desarrolla a partir del inicio de la grieta y se continúa con su propagación y la rotura final.

Inicio

Las grietas que originan la rotura o fractura casi siempre nuclear sobre la superficie en un punto donde existen concentraciones de tensión (originadas por diseño o acabados, ver Factores).

Las cargas cíclicas pueden producir discontinuidades superficiales microscópicas a partir de escalones producidos por deslizamiento de dislocaciones, los cuales actuarán como concentradores de la tensión y, por tanto, como lugares de nucleación de grietas.

Propagación

  • Etapa I: una vez nucleada una grieta, entonces se propaga muy lentamente y, en metales policristalinos, a lo largo de planos cristalográficos de tensión de cizalladura alta; las grietas normalmente se extienden en pocos granos en esta fase.
  • Etapa II: la velocidad de extensión de la grieta aumenta de manera vertiginosa y en este punto la grieta deja de crecer en el eje del esfuerzo aplicado para comenzar a crecer en dirección perpendicular al esfuerzo aplicado. La grieta crece por un proceso de enromamiento y agudizamiento de la punta a causa de los ciclos de tensión.

Rotura

Al mismo tiempo que la grieta aumenta en anchura, el extremo avanza por continua deformación por cizalladura hasta que alcanza una configuración enromada. Se alcanza una dimensión crítica de la grieta y se produce la rotura.

La región de una superficie de fractura que se formó durante la etapa II de propagación puede caracterizarse por dos tipos de marcas, denominadas marcas de playa y estrías. Ambas indican la posición del extremo de la grieta en diferentes instantes y tienen el aspecto de crestas concéntricas que se expanden desde los puntos de iniciación. Las marcas de playa son macroscópicas y pueden verse a simple vista.

Las marcas de playa y estrías no aparecen en roturas rápidas.

Velocidad de propagación

Los resultados de los estudios de fatiga han mostrado que la vida de un componente estructural puede relacionarse con la velocidad de crecimiento de la grieta. La velocidad de propagación de la grieta es una función del nivel de tensión y de la amplitud de la misma.

\frac {da} {dN} = A (\mathcal {4}K)^m

Dónde:

  • A y m son constantes para un determinado material
  • K Factor de intensidad de tensiones
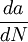  • \frac {da}{dN} pendiente de la curva de velocidad de crecimiento

El valor de m normalmente está comprendido entre 1 y 6.

\mathcal{4}K = K_{max} - K_{min}

o bien

\mathcal{4}K = Y \mathcal {4} \sigma\ \sqrt(\pi\ a)

Desarrollando estas expresiones a partir de gráficas generadas por ellas mismas, se puede llegar a la siguiente ecuación:

N_f = \frac {da}{ A \pi^{\frac {m}{2}} (\mathcal {4} \sigma)^m} \int_{a_0}^{a_c} \frac {1} {Y^m a^{\frac {m}{2}}}\, da

Dónde:

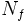  • N_f \ Número de ciclos hasta rotura
  • Y Parámetro independiente de la longitud de la grieta
  • m y A Siguen siendo parámetros definidos por el material
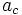  • a_c \ Es la longitud crítica de la grieta
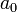  • a_0 \ Longitud de grieta inicial

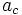a_c \ se puede calcular por:

a_c = (\frac {K_Ic}{\sigma\ Y \sqrt{ \pi\ } })^2

Dónde:

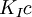  • K_Ic \ Es la tenacidad de fractura de deformaciones planas.

Estas fórmulas fueron generadas por Paul C. Paris en 1961 realizando una gráfica logarítmica log-log de la velocidad de crecimiento de grieta contra el factor de intensidad de tensiones mostrando una relación lineal en la gráfica. Utilizando esta gráfica se pueden realizar predicciones cuantitativas sobre la vida residual de una probeta dado un tamaño de grieta particular. Se encuentra así el comienzo de la iniciación o iniciación rápida de grieta.

Factores que intervienen

Son diversos los factores que intervienen en un proceso de rotura por fatiga a parte de las tensiones aplicadas. Así pues, el diseño, tratamiento superficial y endurecimiento superficial pueden tener una importancia relativa.

Diseño

El diseño tiene una influencia grande en la rotura de fatiga. Cualquier discontinuidad geométrica actúa como concentradora de tensiones y es por donde puede nuclear la grieta de fatiga. Cuanto más aguda es la discontinuidad, más severa es la concentración de tensiones.

La probabilidad de rotura por fatiga puede ser reducida evitando estas irregularidades estructurales, o sea, realizando modificaciones en el diseño, eliminando cambios bruscos en el contorno que conduzcan a cantos vivos, por ejemplo, exigiendo superficies redondeadas con radios de curvatura grandes.

Tratamientos superficiales

En las operaciones de mecanizado, se producen pequeñas rayas y surcos en la superficie de la pieza por acción del corte. Estas marcas limitan la vida a fatiga pues son pequeñas grietas las cuales son mucho más fáciles de aumentar. Mejorando el acabado superficial mediante pulido aumenta la vida a fatiga.

Uno de los métodos más efectivos de aumentar el rendimiento es mediante esfuerzos residuales de compresión dentro de una capa delgada superficial. Cualquier tensión externa de tracción es parcialmente contrarrestada y reducida en magnitud por el esfuerzo residual de compresión. El efecto neto es que la probabilidad de nucleación de la grieta, y por tanto de rotura por fatiga se reduce.

Este proceso se llama «granallado» o «perdigonado». Partículas pequeñas y duras con diámetros del intervalo de 0,1 a 1,0 mm son proyectadas a altas velocidades sobre la superficie a tratar. Esta deformación induce tensiones residuales de compresión.

Endurecimiento superficial

Es una técnica por la cual se aumenta tanto la dureza superficial como la vida a fatiga de los aceros aleados. Esto se lleva a cabo mediante procesos de carburación y nitruración, en los cuales un componente es expuesto a una atmósfera rica en carbono o en nitrógeno a temperaturas elevadas. Una capa superficial rica en carbono en nitrógeno es introducida por difusión atómica a partir de la fase gaseosa. Esta capa es normalmente de 1mm de profundidad y es más dura que el material del núcleo. La mejora en las propiedades de fatiga proviene del aumento de dureza dentro de la capa, así como de las tensiones residuales de compresión que se originan en el proceso de cementación y nitruración.

Influencia del medio

El medio puede afectar el comportamiento a fatiga de los materiales. Hay dos tipos de fatiga por el medio: fatiga térmica y fatiga con corrosión.

Fatiga térmica

La fatiga térmica se induce normalmente a temperaturas elevadas debido a tensiones térmicas fluctuantes; no es necesario que estén presentes tensiones mecánicas de origen externo. La causa de estas tensiones térmicas es la restricción a la dilatación y o contracción que normalmente ocurren en piezas estructurales sometidas a variaciones de temperatura. La magnitud de la tensión térmica resultante debido a un cambio de temperatura depende del coeficiente de dilatación térmica y del módulo de elasticidad. Se rige por la siguiente expresión:

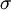\sigma\ = \alpha_{l}\ E \mathcal{4}T

Dónde:

  • \sigma\ \ Tensión térmica
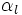  • \alpha_{l}\ \ Coeficiente de dilatación térmica
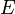  • E \ Modulo de elasticidad
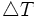  • \mathcal{4}T \ Incremento de temperatura

Fatiga con corrosión

La fatiga con corrosión ocurre por acción de una tensión cíclica y ataque químico simultáneo. Lógicamente los medios corrosivos tienen una influencia negativa y reducen la vida a fatiga, incluso la atmósfera normal afecta a algunos materiales. A consecuencia pueden producirse pequeñas fisuras o picaduras que se comportarán como concentradoras de tensiones originando grietas. La de propagación también aumenta en el medio corrosivo puesto que el medio corrosivo también corroerá el interior de la grieta produciendo nuevos concentradores de tensión.

Enlaces externos

Véase también

Obtenido de "Fatiga de materiales"

Wikimedia foundation. 2010.

Игры ⚽ Поможем сделать НИР

Mira otros diccionarios:

  • Fatiga de materiales — Desde antiguo se sabe que la rotura de los materiales bajo cargas dinámicas se produce más fácilmente que con cargas estáticas. Un ejemplo de ello se tiene en un alambre: flexionándolo repetidamente se rompe con facilidad. Sin embargo, este… …   Enciclopedia Universal

  • Fatiga — ► sustantivo femenino 1 Estado corporal caracterizado por la falta o sensación de falta de fuerzas después de una actividad o un trabajo intensos. SINÓNIMO cansancio 2 Molestia producida por la respiración frecuente o difícil. SINÓNIMO ahogo asma …   Enciclopedia Universal

  • Fatiga — Saltar a navegación, búsqueda El término fatiga puede tener distintos significados según el contexto: La fatiga puede ser una respuesta normal e importante al esfuerzo físico, al estrés emocional, al aburrimiento o la falta de sueño. Sin embargo …   Wikipedia Español

  • Fatiga mental — Saltar a navegación, búsqueda Fatiga mental. La fatiga mental ocasionada por el trabajo se produce básicamente en las personas que tienen un exceso de trabajo de tipo intelectual, donde se exige un gran esfuerzo mental de forma continuada, tales… …   Wikipedia Español

  • fatiga admisible — f Unidad de esfuerzo mбximo permitida para el cбlculo de un elemento estructural, supeditada a la carga de trabajo; las normas de edificaciуn seсalan las fatigas admisibles de los diferentes materiales de construcciуn basados en ensayos de… …   Diccionario de Construcción y Arquitectur

  • fatiga de trabajo — f Unidad de esfuerzo mбximo permitida para el cбlculo de un elemento estructural, supeditada a la carga de trabajo; las normas de edificaciуn seсalan las fatigas admisibles de los diferentes materiales de construcciуn basados en ensayos de… …   Diccionario de Construcción y Arquitectur

  • Ensayos mecánicos de los materiales — Saltar a navegación, búsqueda Cuando un técnico proyecta una estructura metálica, diseña una herramienta o una máquina, define las calidades y prestaciones que tienen que tener los materiales constituyentes. Como hay muchos tipos de aceros… …   Wikipedia Español

  • Límite de fatiga — Curva S N mediante la cual se puede calcular el límite de fatiga. Para la mayoría de los metales existe un esfuerzo crítico, por debajo del cual la rotura sólo se produce al cabo de un considerable período o número de ciclos. Dicho esfuerzo… …   Wikipedia Español

  • Tecnología de materiales — Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas. Puedes añadirlas así o avisar …   Wikipedia Español

  • Propiedades mecánicas de los materiales — Saltar a navegación, búsqueda En ingeniería, las propiedades mecánicas de los materiales son las características inherentes que permiten diferenciar un material de otros, desde el punto de vista del comportamiento mecánico de los materiales en… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”