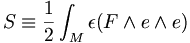Esta página cubre notaciones y definiciones, a veces llamadas el formalismo de Cartan, para el concepto de la conexión de Cartan.

Vierbeins, etcetera

La teoría de las tétradas o vierbein es el caso especial para una variedad diferenciable cuatridimensional. Se aplica a la métrica de cualquier signatura. En cualquier dimensión, para una seudo geometría de Riemann (con signatura métrica (p,q)), esta teoría de la conexión de Cartan es un método alternativo en geometría diferencial. En diversos contextos también se ha llamado método del marco ortonormal, repère mobile, forma de soldaje, forma no holonómica ortonormal.

Esta sección es un acercamiento a las tétradas, pero escrito en términos generales. En otras dimensiones distintas de 4, se han utilizado palabras como tríada, péntada, funfbein, elfbein, etc.. Vielbein cubre todas las dimensiones.

Si se busca una notación de índice base-dependiente, ver tétrada (notación de índice).

los ingredientes básicos

Sea una variedad diferenciable M de dimensión n, y los números naturales fijados p y q con p+q = n. Suponemos dado un SO(p, q) - fibrado principal B sobre M (llamado el fibrado de bases), y un SO(p, q)-fibrado vectorial V asociado a B por medio de la natural representación de SO(p, q) n-dimensional .

Suponga dado también una métrica SO(p, q)-invariante η de signatura (p, q) sobre V; y una función lineal inversible entre fibrados vectoriales sobre M, e: TM → V donde TM es el fibrado tangente de M.

construcciones

Una (seudo)métrica de Riemann se define sobre M como suma amalgamada (push forward) de η por e. Es decir si tenemos dos secciones de TM, X y Y,

g(X, Y)=η(e(X),e(Y)).

Una conexión sobre V, A se define como la única conexión que satisface estas dos condiciones:

• dη(a, b)=η(d_Aa, b)+η(a, d_Ab) para todas las secciones diferenciables a y b de V (es decir d_Aη=0) donde d_A es la derivada exterior covariante. (esto indica básicamente que A se puede ampliar a una conexión sobre el SO(p, q) fibrado principal)

• d_Ae=0. (esto indica básicamente que ∇ definida abajo es libre de torsión)

ahora que hemos especificado A, podemos utilizarla para definir una conexión sobre TM por producto fibrado (pullback) por e;

e(∇X)=d_Ae(X) para todas las secciones diferenciables X de TM.

Dado que lo que ahora tenemos aquí es una SO(p, q) teoría de gauge, la curvatura F de Riemann definida como F = dA + A∧A es covariante de gauge punto a punto. Éste es simplemente el tensor de Riemann de un modo diverso.

la acción de Palatini

En la formulación tétrada de la relatividad general, la acción, como funcional de la cotétrada e y la conexión A sobre la variedad diferenciable M cuatro dimensional viene dada por

donde F es la 2-forma de curvatura de gauge y e es el equivariante antisimétrico reps por tetravectores del Formalismo de Cartan"