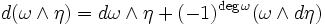Derivada exterior

Derivada exterior

Derivada exterior

En matemáticas, el operador de derivada exterior (o diferencial exterior) de la topología diferencial, amplía el concepto del diferencial de una función a formas diferenciales de un grado más alto. Fue inventado, en su forma actual, por Élie Cartan. La derivada exterior de una forma diferencial de grado k es una forma diferencial de grado k+1. La diferenciación exterior satisface tres propiedades importantes:

d(\omega\wedge\eta) = d\omega\wedge\eta+(-1)^{{\rm deg\,}\omega}(\omega\wedge d\eta)
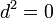  • d^2=0\,, una fórmula que codifica la igualdad de las derivadas parciales cruzadas, de modo que siempre: 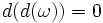d(d(\omega)) = 0\,, para cualquier forma ω

Puede ser demostrado que la derivada exterior está determinada unívocamente por estas propiedades y su coincidencia con el diferencial en 0-formas (funciones).

Los casos especiales de la diferenciación exterior corresponden a los operadores diferenciales familiares del cálculo vectorial a lo largo de las mismas líneas que el diferencial corresponde a gradiente. Por ejemplo, en el espacio euclidiano tridimensional, la derivada exterior de una 1-forma corresponde al rotacional y la derivada exterior de 2-formas corresponde a la divergencia. Esta correspondencia muestra más de una docena de fórmulas del cálculo vectorial como casos especiales de las tres reglas antedichas de la diferenciación exterior. El núcleo del operador 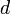d\, consiste en las formas cerradas, y la imagen en las formas exactas (cf. diferenciales exactos).

Véase también

Obtenido de "Derivada exterior"

Wikimedia foundation. 2010.

Игры ⚽ Нужно сделать НИР?

Mira otros diccionarios:

  • Derivada exterior — En matemáticas, el operador de derivada exterior (o diferencial exterior) de la topología diferencial, amplía el concepto del diferencial de una función a formas diferenciales de un grado más alto. Fue inventado, en su forma actual, por Elie… …   Enciclopedia Universal

  • Corchete de Poisson — Saltar a navegación, búsqueda En matemáticas y mecánica clásica, el corchete de Poisson es un importante operador de la mecánica hamiltoniana, actuando como pieza fundamental en la definición de la evolución temporal de un sistema dinámico en la… …   Wikipedia Español

  • Integración — La integral definida de una función representa el área limitada por la gráfica de la función, con signo positivo cuando la función toma valores positivos y negativo cuando toma valores negativos. Para otros usos de este término, véase Integración …   Wikipedia Español

  • Forma diferencial — Saltar a navegación, búsqueda En geometría diferencial, es un objeto matemático perteneciente a un espacio vectorial que aparece en el cálculo multivariable, cálculo tensorial o en física. Comúnmente una forma diferencial puede ser entendida como …   Wikipedia Español

  • Campo de Yang-Mills — Esquema perturbativo de QFT para la interacción de un electrón (e) con un quark (q), la línea azul representa un campo electromagnético (campo de Yang Mills con simetría U(1)) y la línea verde un campo de color (campo de Yang Mills con simetría… …   Wikipedia Español

  • Tensor de campo electromagnético — En electrodinámica clásica y teoría de la relatividad, el tensor de Faraday o tensor de campo electromagnético es un tensor 2 covariante y antisimétrico, cuyas componentes son las componentes de lo que en cada sistema de referencia se reflejan… …   Wikipedia Español

  • Teoría de campo de gauge — Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas. Puedes añadirlas así o avisar …   Wikipedia Español

  • Rotacional — Saltar a navegación, búsqueda En el cálculo vectorial, el rotacional o rotor es un operador vectorial que muestra la tendencia de un campo vectorial a inducir rotación alrededor de un punto. Contenido 1 Introducción 1.1 Fuente vectorial y escalar …   Wikipedia Español

  • Teorema de Stokes — El teorema de Stokes en geometría diferencial es una proposición sobre la integración de formas diferenciales que generaliza varios teoremas del cálculo vectorial. Se nombra así por George Gabriel Stokes (1819 1903), a pesar de que la primera… …   Wikipedia Español

  • Cohomología de de Rham — Saltar a navegación, búsqueda En geometría diferencial, las formas diferenciales en la variedad diferenciable que son derivadas exteriores se llaman exactas; y las formas tales que sus derivadas exteriores son 0 se llaman cerradas (véase formas… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”