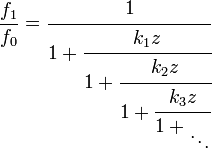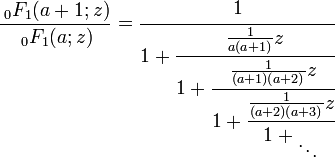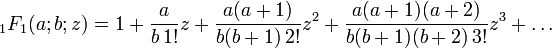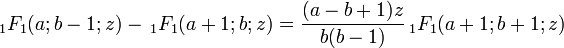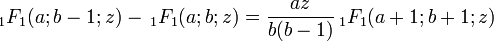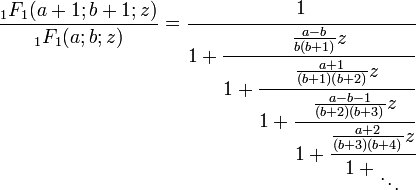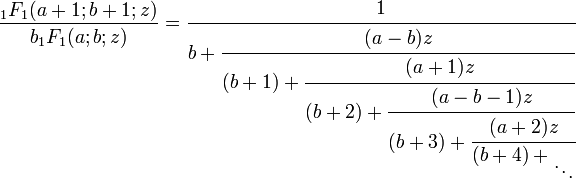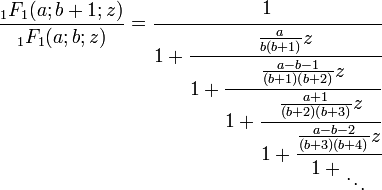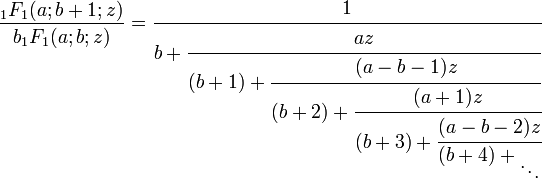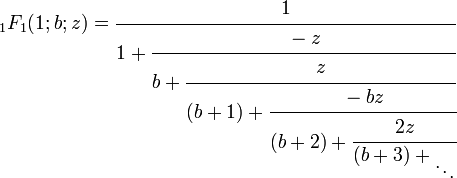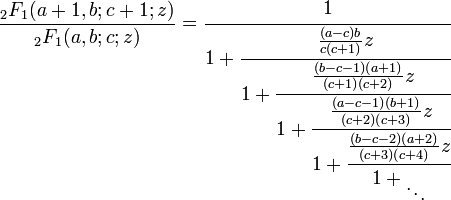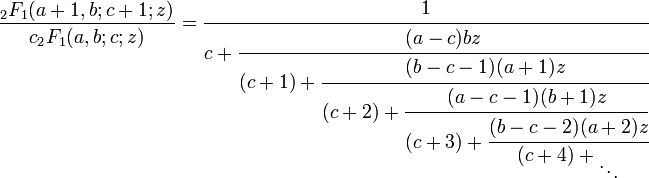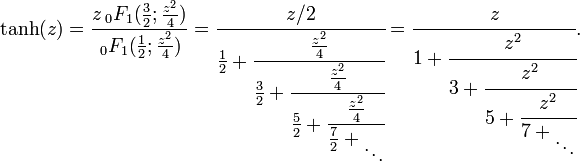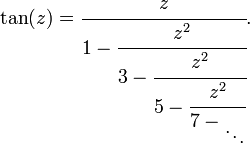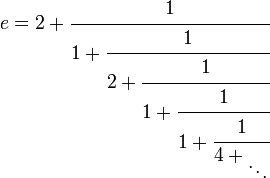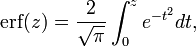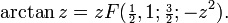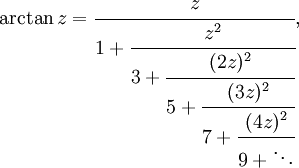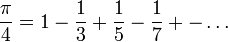- Fracción continua de Gauss
-
Fracción continua de Gauss
En análisis complejo la fracción continua de Gauss es un caso particular de fracción continua generalizada derivada de la serie hipergeométrica. Fue una de las primeras fracciones continuas analíticas conocidas en matemáticas y puede usarse para representar varias funciones elementales importantes, así cómo algunas de las más complicadas funciones trascendentes.
Contenido
Historia
En 1768 Lambert publicó varios ejemplos de fracciones continuas de este tipo y ambos, Euler y Lagrange investigaron construcciones similares,[1] sin embargo fue Gauus quien utilizó el ingenioso desarrollo descrito en la siguiente sección para deducir la forma general de esta fracción continua, en 1813.[2]
Aunque Gauss le dio la forma de esta fracción continua, no ofreció una prueba de sus propiedades de convergencia. Bernhard Riemann[3] y Thomé[4] obtuvieron resultados parciales, pero la demostración final en la región en la que esta fracción continua converge no se obtuvo hasta 1901, por Edward Burr Van Vleck.[5]
Derivación
Sea
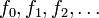 una secuencia de funciones analíticas tales que
una secuencia de funciones analíticas tales que- fi − 1 − fi = kizfi + 1
para todo i > 0, donde cada ki es constante.
Entonces
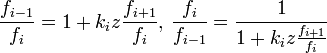 .
.
Estableciendo gi = fi / fi − 1,
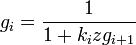 ,
,
Así
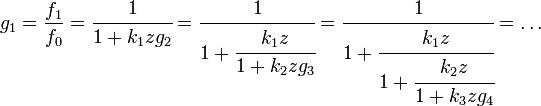 .
.
Repitiendo el razonamiento sucesivamente se obtiene la expresión de la fracción continua
En la fracción continua de Gauss, las funciones fi son funciones hipergeométricas de la forma 0F1, 1F1, y 2F1, y las ecuaciones fi − 1 − fi = kizfi + 1 surgen como identidades entre funciones donde los parámetros difieren en cantidades enteras. Estas identidades pueden probarse de varias formas, por ejemplo, expandiendo la serie y comparando coeficientes, o haciendo las derivadas de varias formas y eliminándolas de las ecuaciones generadas.
La serie 0F1
El caso más simple involucra
 .
.
Comenzando con la identidad
 ,
,
podemos tomar
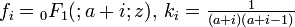 ,
,
dando
o
 .
.
Esta expansión converge a la función meromórfica definida por el cociente entre las dos series convergentes (siempre que, por supuesto, esa a no sea cero, ni un entero negativo).
La serie 1F1
El caso siguiente supone
para lo cual las dos identidades
se usan alternativamente.
Sea
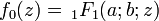 ,
,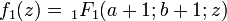 ,
, ,
, ,
,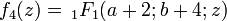 ,
,
etc.
Esto da fi − 1 − fi = kizfi + 1 donde
 , produciendo
, produciendoo
De forma similar
o
Desde 1F1(0;b;z) = 1, pongamos a a 0 y reemplacemos b + 1 con b en la primera fracción continua se obtiene un caso especial simplificado:
La serie 2F1
El caso final supone
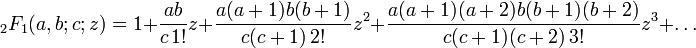 .
.
De nuevo, se usan dos identidades alternativamente.
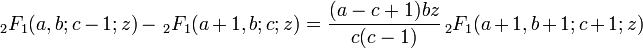 ,
,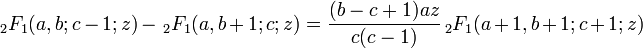 .
.
Estas son, esencialmente, la misma identidad con a y b intercambiadas.
Sea
 ,
, ,
,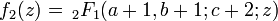 ,
, ,
, ,
,
etc.
Esto proporciona fi − 1 − fi = kizfi + 1 donde
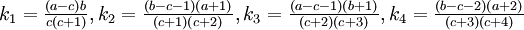 , produciendo
, produciendoo
Desde 2F1(0,b;c;z) = 1, damos a a el valor 0 y reemplazamos c + 1 con c obteniéndose un caso especial simplificado de la fracción continua:
Propiedades de convergencia
En esta sección, los casos donde uno o más de los parámetros es un entero negativo se excluye, en virtud de que en estos casos o bien la serie hipergeométrica no está definida o bien son polinomios por lo que la fracción continua se acaba. Se excluyen también otras excepciones triviales.
En los casos 0F1 y 1F1, la serie converge por doquier así que la fracción de la izquierda es una función meromórfica. Las fracciones continuas de la derecha convergerán uniformemente en cualquier conjunto cerrado que no contenga polos de esta función.[6]
En el caso 2F1, el radio de convergencia de la serie es 1 y la fracción de la izquierda es una función meromórfica en este círculo. Las fracciones continuas de la derecha convergerán a la función por doquier dentro de este círculo.
Fuera del círculo, la fracción continua representa la extensión analítica de la función a el plano complejo con el eje real positivo, desde Plantilla:Math a el punto eliminado en infinito . En la mayoría de los casos Plantilla:Math es una rama puntual y la línea desde Plantilla:Math a más infinitoes una rama cortada para esta función. La fracción continua converge a una función meromórfica en este dominio y converge uniformemente en cualquier subconjunto finito cerrado de este dominio que no contenga polos.[7]
Aplicaciones
La serie 0F1
Tenemos
 ,
, ,
,
por tanto
Esta expansión particular se conoce como fracción continua de Lambert y data de 1768.[8]
Fácilmente se sigue que
La expansión de tanh puede usarse para probar que en es irracional para cualquier entero n (lo cual no es suficiente, desgraciadamente, para probar que e es un número trascendente). La expansión de tan fue usada por Lambert y Legendre para probar que π es irracional.
La función de Bessel Jν puede escribirse
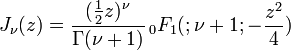 ,
,
de lo cual, se sigue que
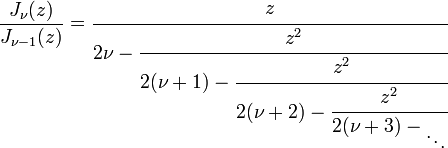 .
.
Estas fórmulas también son válidad para cualquier complejo z.
La serie 1F1
Desde ez = 1F1(1;1;z), 1 / ez = e − z
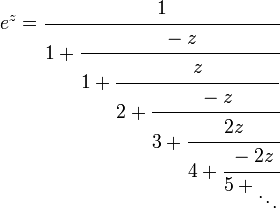
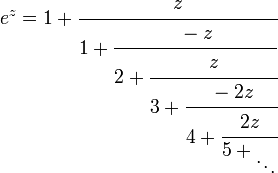 .
.
Con alguna manipulación, esto puede usarse para probar la representación en fracción simple continua de e,
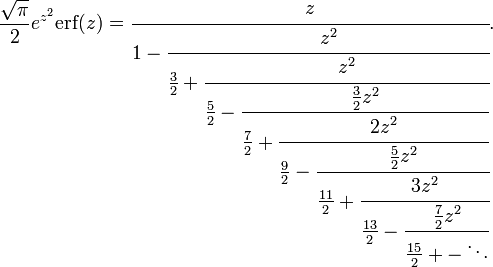
La función error erf (z), dada por
puede también calcularse en términos de la función hipergeométrica de Kummer:
Mediante la aplicación de la fracción continua de Gauss puede obtenerse una útil expansión válida para todo número complejo z:[9]
Un argumento similar puede hacerse para derivar expansiones de fracciones continuas para la integral de Fresnel, para la función Dawson y para la función gamma incompleta. Una versión más simple del argumento da paso a dos útiles expansiones de fracción continua de la función exponencial.[10]
La serie 2F1
Desde
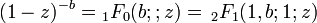 ,
,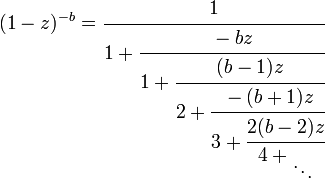
Se muestra fácilmente que la expansión en serie de Taylor de arcotangente de z en un entorno de cero viene dada por:
La fracción continua de Gauss puede aplicarse a esta identidad, dando paso a la expansión
que converge a la rama principal de la función inversa de la tangente en el plano complejo , con el cut extendiéndose a lo largo de el eje imaginario desde i hasta el punto en infinito y desde -i hasta el punto en infinito.[11]
Esta fracción continua particular converge clara y rápidamente cuando z = 1, dando el valor de π/4 con siete decimales hacia el noveno convergente. La serie correspondiente
converge mucho más lentamente, necesitándose más de un millón de términos para dar lugar a siete decimales de exactitud.[12]
Algunas variaciones de este argumento se pueden usar para producir expansiones de fracciones continuas para el logaritmo natural, la función arcoseno y la serie binomial generalizada.
Referencias
- ↑ Jones & Thron (1980) p. 5
- ↑ C. F. Gauss (1813), Werke, vol. 3 pp. 134-138.
- ↑ B. Riemann (1863), "Sullo svolgimento del quoziente di due serie ipergeometriche in frazione continua infinita" en Werke. pp. 400-406. (Posthumous fragment).
- ↑ L. W. Thomé (1867), "Über die Kettenbrüchentwicklung des Gaussen quotienten …," Jour. für Math. vol. 67 pp. 299-309.
- ↑ E. B. Van Vleck (1901), "On the convergence of the continued fraction of Gauss and other continued fractions." Annals of Mathematics, vol. 3 pp. 1-18.
- ↑ Jones & Thron (1980) p. 206
- ↑ Wall, 1973 (p. 339)
- ↑ Wall (1973) p. 349.
- ↑ Jones & Thron (1980) p. 208.
- ↑ Véase el ejemplo en el artículo Padé table para las expansiones de ez como fracciones continuas de Gauss.
- ↑ Wall (1973) p. 343. Notice that i and −i are branch points for the inverse tangent function.
- ↑ Jones & Thron (1980) p. 202.
- Jones, William B.; Thron, W. J. (1980). Continued Fractions: Theory and Applications. Reading, Massachusetts: Addison-Wesley Publishing Company, pp. 198-214. ISBN 0-201-13510-8.
- Wall, H. S. (1973). Analytic Theory of Continued Fractions. Chelsea Publishing Company, pp. 335-361. ISBN 0-8284-0207-8.
(This is a reprint of the volume originally published by D. Van Nostrand Company, Inc., in 1948.)
Categoría: Análisis matemático
Wikimedia foundation. 2010.