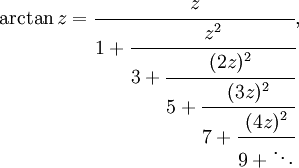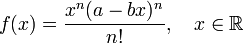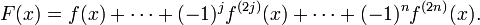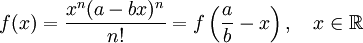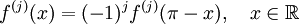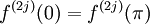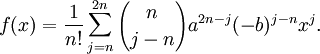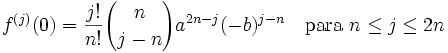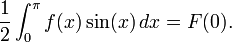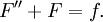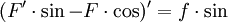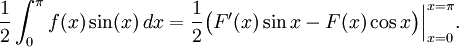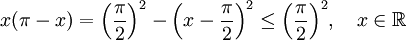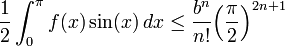Aunque la constante matemática conocida como π (pi) ha sido estudiada desde la antigüedad, y también el concepto de número irracional, no fue sino hasta el siglo XVIII que se probó la irracionalidad de π.

En el siglo XX, se encontraron demostraciones que no requerían un conocimiento más allá del cálculo integral. Una de éstas es muy conocida, encontrada por Ivan Niven.

En este artículo se muestran unas cuantas demostraciones, incluida la de Ivan Niven.

Contenido 1 Demostración mediante fracciones continuas 2 Demostración de Ivan Niven 3 Véase también 4 Referencias

Demostración mediante fracciones continuas

Se puede demostrar que π es irracional fácilmente si éste es expresable mediante una fracción continua infinita.^[1] Dado que cada fracción continua finita se puede expresar mediante un número racional y viceversa,^[1] si π fuera racional, debería existir tal fracción continua. Veamos que tal fracción continua es infinita:

• La función arcotangente se puede representar en forma de fracción continua de Gauss, de la siguiente manera:

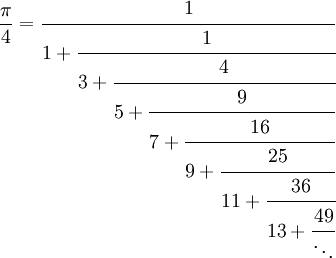
• Tomando z=1, obtenemos que 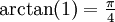y por tanto:

Si 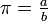, entonces 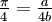y la fracción continua tendría un número finito n de términos. Puesto que esta fracción continua tiene una estructura ordenada, es fácil comprobar que ésta contiene infinitos términos, probando la irracionalidad de π.

Demostración de Ivan Niven

La demostración se basa en el método de reducción al absurdo.^[2] Supongamos que π = a/b, con a,b enteros y b ≠ 0 , los cuales, sin pérdida de generalidad diremos que son positivos. Entonces la demostración consiste en los siguientes pasos:

• Dado cualquier número natural n, se define la siguiente función polinómica:

Y denotaremos como

a la suma alternada de f(x) y sus primeras n derivadas pares.

• Principio 1: F(0) = F(π).

Puesto que

y dado que suponemos π = a/b, la regla de la cadena y el principio de inducción implican que

para todas las derivadas, en particular

para todo j = 1, 2, ...,n.

• Principio 2: F(0) es un entero.

Usando el binomio de Newton para expandir (a – bx)ⁿ y haciendo un cambio de índice j = k + n, obtenemos las representación

Dado que los coeficientes x⁰, x¹, ..., x^n − 1 son cero y el grado del polinomio f es a lo sumo 2n, nosotros tenemos que f ^(j)(0) = 0 para j < n y j > 2n. Más aún,

Puesto que j ≥ n, la fracción de estos dos factoriales es un entero. Lo mismo se cumple para el coeficiente binomial, que puede ser visto como una interpretación combinacional del triángulo de Pascal. Y así f y cualquier derivada de f en 0 es un entero, con lo cual F(0) también lo será.

• Principio 3:

Dado que f ^(2n + 2) es el polinomio cero, tenemos que

La derivadas de la función seno y coseno están dados por (sin(x))' = cos(x) y (cos(x))' = −sin(x), y así la regla del producto implica

Por el teorema fundamental del cálculo

Ahora bien, sin(0) = sin(π) = 0 y cos(0) = –cos(π) = 1, y aplicando el principio 1 se obtiene el resultado deseado.

• Prueba: Puesto que f(x) > 0 y sin(x) > 0 para 0 < x < π (porque π es el más pequeño número positivo que anula la función seno), el pincipio 2 y 3 muestran que F(0) es un entero positivo . Luego

y 0 ≤ sin(x) ≤ 1 para 0 ≤ x ≤ π, obtenemos que

que es más pequeño que 1 para un entero n grande, y también F(0) < 1 por el principio 3 para ese n, lo cual es imposible para el entero positivo F(0).

Q.E.D.

Véase también

• Número π
• Número e
• Demostración de que e es irracional

Referencias

1. ↑ ^{a b} Wolffram.Mathworld.com (2008). «Continued fraction.». Consultado el 17 de mayo de 2008.
2. ↑ Niven,Ivan (1947). «A simple proof that π is irrational» Bull. Amer. Math. Soc. Vol. 56. n.º 6. p. 509.

Harold Jeffreys, Scientific Inference, 3rd edition, Cambridge University Press, 1973, page 268.