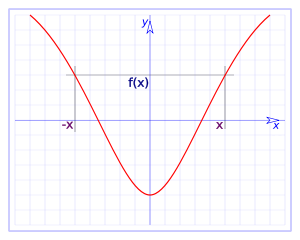
Función par

Función par
Gráfica de una función par.

En matemáticas, una función par es cualquier función que satisface la relación f(x) = f(-x)\, para todo valor admisible de x. La gráfica de dicha función es simétrica respecto al eje y.

Contenido

Definición formal

El término función par suele referirse a una clase especial de funciones de variable real: una función f : \mathbf{R}\to \mathbf{R} es una función par si para x\in\mathbf{R} se cumple la siguiente relación:

f(x) = f(-x)\,.

La definición anterior puede generalizarse a funciones sobre dominios más generales. Si A es un conjunto con cierta estructura algebraica en la que existan inversos aditivos (por ejemplo, los números complejos C), una función par sería toda función f:A\to B que cumpla:

f(a) = f(-a)\ , \forall a \in A.

Aunque asimétrica a primera vista, dicha definición de función par presupone que si a\in A entonces necesariamente -a \in A, de no ser así no se podría definir f( − a).

Ejemplo

La función f(x) = x2 + 1 es par ya que para cualquier valor de x se cumple ( − x)2 + 1 = (x)2 + 1. Por ejemplo:

f( − 2) = ( − 2)2 + 1 = 4 + 1 = 5 = 22 + 1 = f(2).

Véase también

Enlaces externos


Wikimedia foundation. 2010.

Игры ⚽ Нужно сделать НИР?

Mira otros diccionarios:

  • Función impar — En matemáticas, una función impar es cualquier función que satisface la relación para todo valor admisible de x. La gráfica de dicha función es simétrica con respecto al origen de coordenadas. Ejemplos …   Wikipedia Español

  • Par — o PAR puede referirse a: Contenido 1 Acrónimo 2 Biografías 3 Biología 4 Cultura 5 Física …   Wikipedia Español

  • Función matemática — En la imagen se muestra una función entre un conjunto de polígonos y un conjunto de números. A cada polígono le corresponde su número de lados. En matemáticas, se dice que una magnitud o cantidad es función de otra si el valor de la primera… …   Wikipedia Español

  • Función real — Una función real es una función matemática cuyo dominio y codominio están contenidos en , es decir, es una función: En general se trata de funciones continuas, o bien discontinuas cuando están representadas por tramos, a diferencia de las… …   Wikipedia Español

  • Función hermítica — En análisis matemático, una función hermítica es una función compleja que tiene la propiedad de que su conjugada es igual a la función original con la variable cambiada de signo: para todo x en el dominio de f. Esta definición se puede extender a …   Wikipedia Español

  • Función — (Del lat. functio, onis.) ► sustantivo femenino 1 BIOLOGÍA Actividad o capacidad de acción específica de un ser vivo y de sus órganos: ■ la función del riñón; la función clorofílica. 2 Desempeño de un cargo u oficio: ■ el vicepresidente desempeña …   Enciclopedia Universal

  • par — (Del lat. par, paris.) ► adjetivo 1 Igual o semejante a otro en cantidad, calidad u otra característica: ■ es un producto par en precio al otro. SINÓNIMO parejo 2 ZOOLOGÍA Se aplica al órgano que corresponde de forma simétrica a otro igual. 3… …   Enciclopedia Universal

  • Función polinómica de grado 2 — Saltar a navegación, búsqueda De vital importancia en matemáticas y física es la función cuadrática o de segundo grado. Una función polinómica de grado dos o función cuadrática es la que corresponde a un polinomio en x de segundo grado, según la… …   Wikipedia Español

  • Par de Cooper — Saltar a navegación, búsqueda En superconductividad se conoce como par de Cooper a la pareja de electrones que se hallan ligados debido a que en el estado superconductor ambas partículas se comportan como si se atrayeran, pese a tener ambos carga …   Wikipedia Español

  • Par de Lax — Saltar a navegación, búsqueda En la mecánica clásica el estado de un sistema se especifica por un punto en el espacio fase o espacio fásico. En general es un espacio de dimensión par con coordenadas de posición y momento . La evolución del… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”