Función parcial

Función parcial
 Se ha sugerido que este artículo o sección sea fusionado con función total (discusión).
Una vez que hayas realizado la fusión de artículos, pide la fusión de historiales aquí.
Ejemplo de una función parcial que no es una función total.
Ejemplo de una función total.

Una función parcial es una relación que asocia a cada elemento de un conjunto (a veces denominado dominio) con, como máximo, uno de los elementos de otro conjunto (que puede ser el mismo), llamado codominio. En cualquier caso, no es necesario que todos los elementos del dominio estén asociados con algún elemento del codominio.

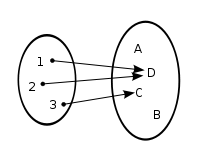
Si todos los elementos de un conjunto X se asocian con un elemento de Y mediante una función parcial f:X→Y , entonces se dice que f es una función total, o simplemente una función, como se entiende tradicionalmente este concepto en matemáticas. No todas las funcionas parciales son funciones totales.

Discusión y ejemplos

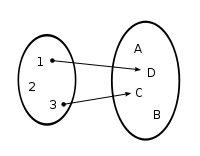
El primero de los diagramas mostrados representa una función parcial; no es una función total porque el elemento 2 en el conjunto de la izquierda no está asociado con ningún elemento del conjunto de la derecha.

Considérese la función del Logaritmo natural, que relaciona el conjunto de los Números Reales consigo mismo. El logaritmo de un número real negativo no es un número real, así que el logaritmo natural no asocia a todos los elementos del codominio con un elemento del dominio. Por lo tanto, el logaritmo natural no es una función total cuando se la considera como una función del conjunto de números reales consigo misma, sino una función parcial. Si el dominio se restringiera al conjunto de los reales positivos, entonces si se trataría de una función total.


Wikimedia foundation. 2010.

Игры ⚽ Нужно сделать НИР?

Mira otros diccionarios:

  • Función recursiva — En lógica matemática y computación, las funciones recursivas o también conocidas como funciones recursivas μ son una clase de funciones de los números naturales en los números naturales que son «computables» en un sentido intuitivo. De hecho, en… …   Wikipedia Español

  • Función total — Se ha sugerido que este artículo o sección sea fusionado con función parcial (discusión). Una vez que hayas realizado la fusión de artículos, pide la fusión de historiales aquí. En matemáticas, una función se dice que es total si está definida… …   Wikipedia Español

  • Función computable — Las funciones computables son el objeto básico de estudio de la teoría de la computabilidad y son, específicamente, las funciones que pueden ser calculadas por una máquina de Turing. Contenido 1 Introducción 2 Definición 3 Comentarios …   Wikipedia Español

  • Función monótona — En matemáticas, una función entre conjuntos ordenados se dice monótona (o isótona) si conserva el orden dado. Las funciones de tal clase surgieron primeramente en cálculo, y fueron luego generalizadas al entorno más abstracto de la teoría del… …   Wikipedia Español

  • Función cuantil — En probabilidad la función cuantil de una distribución de probabilidad es la inversa de la función de distribución.[1] Dada una función de distribución continua y estrictamente monótona, , la función cuantil, F −1, devuelve un valor x tal… …   Wikipedia Español

  • Función racional — Este artículo trata sobre el concepto matemático. Para la «capacidad de razonar», véase Racionalidad. Función racional de grado 2 …   Wikipedia Español

  • Derivada parcial — Saltar a navegación, búsqueda En matemática, una derivada parcial de una función de diversas variables es su derivada respecto a una de esas variables manteniendo las otras, constantes. Las derivadas parciales son útiles en cálculo vectorial y… …   Wikipedia Español

  • Traza parcial — En el álgebra lineal y el análisis funcional, la traza parcial es una generalización de la traza. Mientras que la traza es una función a valores escalares sobre operadores, la traza parcial es una función operador valorada. La traza parcial tiene …   Wikipedia Español

  • Derivada parcial — Definición Cuando una magnitud A es función de diversas variables (x,y,z,...), es decir: A = f(x,y,z...) se entiende como derivada parcial de A respecto de una variable a la expresión obtenida al …   Enciclopedia Universal

  • Producto de Euler para la función zeta de Riemann — Saltar a navegación, búsqueda En 1737 Leonhard Euler probó un resultado que abrió las puertas de la moderna teoría de números ( teoría analítica de números ) enunciando el siguiente teorema: Si s > 1, entonces …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”