Función monótona

En matemáticas, una función entre conjuntos ordenados se dice monótona (o isótona) si conserva el orden dado. Las funciones de tal clase surgieron primeramente en cálculo, y fueron luego generalizadas al entorno más abstracto de la teoría del orden. Aunque los conceptos generalmente coinciden, las dos disciplinas han desarrollado una terminología ligeramente diferente; mientras en cálculo se habla de funciones monótonamente crecientes y monótonamente decrecientes (o simplemente crecientes y decrecientes), en la teoría del orden se usan los términos monótona y antítona, o se habla de funciones que conservan e invierten el orden.

Contenido

1 Definición general
2 Monotonicidad en cálculo y análisis
- 2.1 Ejemplo gráfico
- 2.2 Aplicaciones y resultados básicos
3 Funciones booleanas
4 Véase también

Definición general

Sea

$f:P\to Q$

una función entre dos conjuntos P y Q, donde cada conjunto tiene un orden parcial (los dos se denotarán por ≤). En cálculo se habla de funciones entre subconjuntos de los reales, y el orden ≤ no es otro que el orden usual de la recta real, aunque esto no es esencial para la definición.

La función f es monótona si y sólo si x ≤ y implica f(x) ≤ f(y) (es decir, la función es creciente), o bien x ≤ y implica f(x) ≥ f(y) (es decir, la función es decreciente). En otras palabras, una función es monótona si conserva el orden.

Monotonicidad en cálculo y análisis

En cálculo no hay usualmente necesidad de invocar los métodos abstractos de la teoría del orden. Como ya se señaló, las funciones se establecen entre (subconjuntos de) números reales, ordenados de forma natural.

Por la forma de la gráfica de una función monótona en los reales, tales funciones se llaman también monótonamente crecientes (o no decreciente), respectivamente.

Ejemplo gráfico

A continuación se muestran tres gráficas de funciones cualesquiera. La primera de ellas es una función estrictamente creciente, ya que conserva el órden ascendente durante todo el recorrido de la función. La segunda de ellas es escrictamente decreciente, puesto que conserva el órden descendente durante todo el recorrido de la función. La última de ellas es una función con un recorrido con partes donde la función es creciente y partes donde es decreciente (presenta máximos y mínimos relativos).

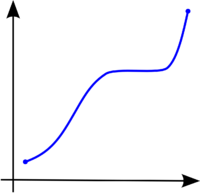
Función monótona creciente.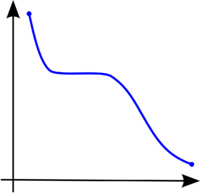

Función monótona decreciente.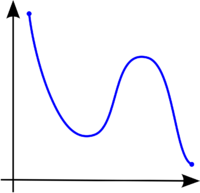

Función no monótona.

Aplicaciones y resultados básicos

Monotonía En matemáticas, cada una de las siguientes propiedades de una función f : R → R implica la siguiente:

f es monótona.
f tiene un límite por la izquierda y por la derecha en cualquier punto de su dominio de definición.
f sólo puede tener discontinuidades de salto.
f sólo puede tener una cantidad enumerable de discontinuidades.

Estas propiedades son la razón por la que las funciones monótonas son útiles en el análisis matemático. Dos importantes hechos que se deducen de que una función sea monótona son:

Si f es una función monótona definida en un intervalo I, entonces f es derivable casi siempre en I, es decir, el conjunto de puntos x en I en donde f no es diferenciable tiene medida de Lebesgue 0.
Si f es una función monótona definida en un intervalo [a, b], entonces f es Riemann-integrable.

Una importante aplicación de las funciones monótonas es en probabilidad. Si X es una variable aleatoria, su función de distribución

$F_X(x)=P(X\le x)$

es una función creciente.

Funciones booleanas

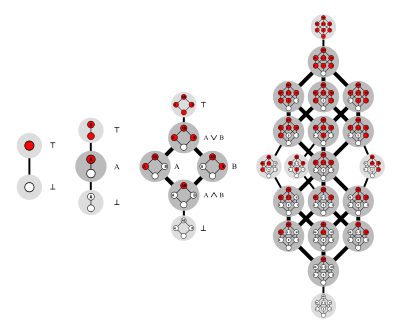
Los retículos distributivos libres de funciones booleanas monótonas sobre 0, 1, 2 y 3 argumentos.

En el álgebra de Boole, una función monótona es una tal que para todo a_i y b_i en {0,1} tales que a₁ ≤ b₁, a₂ ≤ b₂, ... , a_n ≤ b_n

es cierto que se cumple

f(a₁, ... , a_n) ≤ f(b₁, ... , b_n).

Las funciones booleanas monótonas son precisamente aquellas que pueden ser definidas como una composición de conjunciones y disyunciones, pero sin negaciones.

El número de estas funciones sobre n variables es conocido como el número de Dedekind de n.

Véase también

Categorías:

Teoría del orden
Tipos de funciones

Wikimedia foundation. 2010.

Игры ⚽ Нужно сделать НИР?

Mira otros diccionarios:

Función matemática — En la imagen se muestra una función entre un conjunto de polígonos y un conjunto de números. A cada polígono le corresponde su número de lados. En matemáticas, se dice que una magnitud o cantidad es función de otra si el valor de la primera… … Wikipedia Español
Función real — Una función real es una función matemática cuyo dominio y codominio están contenidos en , es decir, es una función: En general se trata de funciones continuas, o bien discontinuas cuando están representadas por tramos, a diferencia de las… … Wikipedia Español
Función — (Del lat. functio, onis.) ► sustantivo femenino 1 BIOLOGÍA Actividad o capacidad de acción específica de un ser vivo y de sus órganos: ■ la función del riñón; la función clorofílica. 2 Desempeño de un cargo u oficio: ■ el vicepresidente desempeña … Enciclopedia Universal
Función de producción — La función de producción representa la máxima cantidad que se puede producir de un bien con unos recursos; por lo tanto es una aplicación que a un vector de recursos le hace corresponder un escalar que representa la cantidad producida. La función … Wikipedia Español
Función booleana 2-monótona — En matemáticas, una función booleana 2 monótona (más conocida en inglés como 2 monotone boolean function) es una función booleana monótona ƒ : {0,1}n → {0,1}, para la cual existe un ordenamiento lineal de sus variables w1, w2, ..., wn, de… … Wikipedia Español
Función cuantil — En probabilidad la función cuantil de una distribución de probabilidad es la inversa de la función de distribución.[1] Dada una función de distribución continua y estrictamente monótona, , la función cuantil, F −1, devuelve un valor x tal… … Wikipedia Español
Función de Cantor — En matemáticas, la función de Cantor, llamada así en honor de Georg Cantor, es un ejemplo de función matemática que es continua pero no absolutamente continua. También se la conoce como la escalera del Diablo. La función de Cantor guarda una… … Wikipedia Español
Función de utilidad — Una función de utilidad es una función real que mide la satisfacción o utilidad obtenida por un consumidor cuando disfruta vía consumo de cierta cantidad de bienes. Matemáticamente puede demostrarse que si es posible modelizar la conducta de un… … Wikipedia Español
Función booleana regular — En matemáticas, una función booleana regular es una clase particular de funciones booleanas que toma en cuenta el ordenamiento de sus distintos parámetros. Estas funciones son útiles en muchas áreas de la matemática aplicada, tales como la… … Wikipedia Español
Función de supervivencia — En análisis de la supervivencia se llama función de supervivencia, también conocida en ingeniería como función de fiabilidad, a la función que mide la probabilidad de que un sujeto sobreviva más allá de un periodo de tiempo dado. La función de… … Wikipedia Español

Los diccionarios y las enciclopedias sobre el Académico

Función monótona

Contenido

Definición general