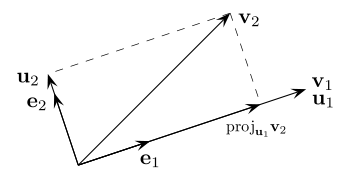
Proceso de ortogonalización de Gram-Schmidt

Proceso de ortogonalización de Gram-Schmidt

En álgebra lineal, el proceso de ortogonalización de Gram–Schmidt es un algoritmo para construir, a partir de un conjunto de vectores linealmente independientes de un espacio prehilbertiano (usualmente, el espacio euclídeo Rn), otro conjunto ortonormal de vectores que genere el mismo subespacio vectorial.

Este algoritmo recibe su nombre de los matemáticos Jørgen Pedersen Gram y Erhard Schmidt.

Descripción del algoritmo de ortonormalización de Gram–Schmidt

Los dos primeros pasos del proceso de Gram–Schmidt

Se define, en primer lugar, el operador proyección mediante

\mathrm{proj}_{\mathbf{u}}\,\mathbf{v} = {\langle \mathbf{v}, \mathbf{u}\rangle\over\langle \mathbf{u}, \mathbf{u}\rangle}\mathbf{u} = {\langle \mathbf{v}, \mathbf{u}\rangle\over||\mathbf{u}||^{2}}\mathbf{u}, = {||\mathbf{v}|| _\dot\ ||\mathbf{u}|| _\dot\ \cos\alpha \over ||\mathbf{u}||}{\mathbf{u} \over ||\mathbf{u}||} = ||\mathbf{v}||\cos\alpha {\mathbf{u} \over ||\mathbf{u}||},

donde los corchetes angulares representan el producto interior. Es evidente que

\mathbf{v}-\mathrm{proj}_{\mathbf{u}}\,\mathbf{v}

es un vector ortogonal a \mathbf{u}. Entonces, dados los vectores \mathbf{v}_1, \dots, \mathbf{v}_n, el algoritmo de Gram–Schmidt construye los vectores ortonormales \mathbf{e}_1, \dots, \mathbf{e}_n de la manera siguiente:

\mathbf{u}_1 = \mathbf{v}_1, \mathbf{e}_1 = {\mathbf{u}_1 \over ||\mathbf{u}_1||}
\mathbf{u}_2 = \mathbf{v}_2-\mathrm{proj}_{\mathbf{u}_1}\,\mathbf{v}_2, \mathbf{e}_2 = {\mathbf{u}_2 \over ||\mathbf{u}_2||}
\mathbf{u}_3 = \mathbf{v}_3-\mathrm{proj}_{\mathbf{u}_1}\,\mathbf{v}_3-\mathrm{proj}_{\mathbf{u}_2}\,\mathbf{v}_3, \mathbf{e}_3 = {\mathbf{u}_3 \over ||\mathbf{u}_3||}
\vdots \vdots
\mathbf{u}_k = \mathbf{v}_k-\sum_{j=1}^{k-1}\mathrm{proj}_{\mathbf{u}_j}\,\mathbf{v}_k, \mathbf{e}_k = {\mathbf{u}_k\over||\mathbf{u}_k||}

A partir de las propiedades de la proyección y del producto escalar, es sencillo probar que la sucesión de vectores \mathbf{u}_1, \dots, \mathbf{u}_n es ortonormal.

Ejemplo

Considera el siguiente conjunto de vectores en R2 (con el convencional producto interno)

S = \left\lbrace\mathbf{v}_1=\begin{pmatrix} 3 \\ 1\end{pmatrix}, \mathbf{v}_2=\begin{pmatrix}2 \\2\end{pmatrix}\right\rbrace.

Ahora, aplicamos Gram–Schmidt, para obtener un conjunto de vectores ortogonales:

\mathbf{u}_1=\mathbf{v}_1=\begin{pmatrix}3\\1\end{pmatrix}
\mathbf{u}_2 = \mathbf{v}_2 - \mathrm{proj}_{\mathbf{u}_1} \, \mathbf{v}_2 = \begin{pmatrix}2\\2\end{pmatrix} - \mathrm{proj}_{({3 \atop 1})} \, {\begin{pmatrix}2\\2\end{pmatrix}} = \begin{pmatrix} -2/5 \\6/5 \end{pmatrix}.

Verificamos que los vectores u1 y u2 son de hecho ortogonales:

\langle\mathbf{u}_1,\mathbf{u}_2\rangle = \left\langle \begin{pmatrix}3\\1\end{pmatrix}, \begin{pmatrix}-2/5\\6/5\end{pmatrix} \right\rangle = -\frac65 + \frac65 = 0.

Entonces podemos normalizar los vectores dividiendo por su norma como hemos mostrado anteriormente:

\mathbf{e}_1 = {1 \over \sqrt {10}}\begin{pmatrix}3\\1\end{pmatrix}
\mathbf{e}_2 = {1 \over \sqrt{40 \over 25}} \begin{pmatrix}-2/5\\6/5\end{pmatrix} = {1\over\sqrt{10}} \begin{pmatrix}-1\\3\end{pmatrix}.

Enlaces externos


Wikimedia foundation. 2010.

Игры ⚽ Нужно сделать НИР?

Mira otros diccionarios:

  • Gram (desambiguación) — La palabra Gram puede hacer referencia a varias cosas diferentes: a Gram, en la mitología escandinava el nombre de la espada que Sigfrido usó para matar al dragón Fafner; a Gram, un municipio y localidad en la península de Jutlandia (Dinamarca);… …   Wikipedia Español

  • Factorización de matrices — Saltar a navegación, búsqueda En álgebra lineal la factorización de una matriz es la descomposición de la misma como producto de dos o más matrices según una forma canónica. Según las aplicaciones de la factorización podemos distinguir los… …   Wikipedia Español

  • Factorización QR — Saltar a navegación, búsqueda En álgebra lineal, la descomposición o factorización QR de una matriz es una descomposición de la misma como producto de una matriz ortogonal por una triangular superior. La descomposición QR es la base del algoritmo …   Wikipedia Español

  • Vector unitario — En álgebra lineal y Física, un vector unitario o versor es un vector de módulo uno. En ocasiones se lo llama también vector normalizado. Contenido 1 Notación 2 Definición 3 Versor asociado a un vector …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”