- Ángulo interior
-
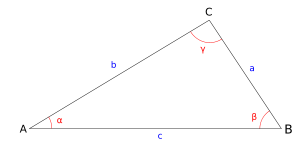Un triángulo tiene tres ángulos interiores, marcados en la figura como α, β y γ.
En geometría, un ángulo interior o ángulo interno es un ángulo formado por dos lados de un polígono que comparten un extremo común y que está contenido dentro del polígono. Un polígono simple tiene exactamente un ángulo interno por cada vértice y está situado del lado opuesto del polígono.
Si todos los ángulos interiores de un polígono no superan los 180 grados o π radianes, se clasifican como polígonos convexos. Si existe por lo menos un ángulo superior a 180 grados o π radianes, se trata de un polígono cóncavo.
Si todos los ángulos interiores de un polígono convexo son iguales y todos sus lados tienen la misma longitud, se trata de un polígono regular. En caso contrario, se trata de un polígono irregular.
Suma de los ángulos interiores de un polígono regular
La suma de los ángulos interiores de un polígono regular tiene un valor que depende del número de lados del polígono y se mantiene constante para cualquier combinación de valores de los ángulos internos. El valor de esta suma en grados puede conocerse aplicando la fórmula:
Donde "n" es igual a los lados de un poligono
Por tanto la medida en grados de uno solo de éstos ángulos equivale a:
Véase también
Enlaces externos
- Rodríguez, R.A. (3 de octubre de 2010). «Recta de Euler». Consultado el 13 de octubre de 2010. «Demostración interactiva realizada con GeoGebra (en Java)».
Categorías:- Ángulos
- Polígonos
Wikimedia foundation. 2010.
