Onda elástica

Onda elástica

Una onda elástica es una perturbación tensional que se propaga a lo largo de un medio elástico. Por ejemplo las ondas sísmicas ocasionan temblores que pueden tratarse como ondas elásticas que se propagan por el terreno.

Contenido

Ecuación de movimiento

En un medio elástico no corrido a fuerzas sonoras de volumen la ecuación de movimiento de una onda elástica que relaciona la velocidad de propagación con las tensiones existentes en el medio elástico vienen dadas, usando el convenio de sumación de Einstein, por:

(1) \frac{\part \sigma_{ij}}{\part x_j} = \rho \left(\frac{\part v_i}{\part t} + v_j\frac{\part v_i}{\part x_j} \right)

Donde \rho\, es la densidad y el término entre paréntesis del segundo término coincide con la aceleración o derivada segunda del desplazamiento. Reescribiendo la ecuación anterior en términos de los desplazamientos producidos por la onda elástica, mediante las ecuaciones de Lamé-Hooke y las relaciones del tensor deformación con el vector desplazamiento, tenemos:

(2a) \frac{E}{2(1+\nu)}\frac{\part^2 u_i}{\part x_k^2} + \frac{E}{2(1+\nu)(1-2\nu)}\frac{\part^2 u_k}{\part x_k \part x_i} = \rho \ddot{u}_i

Que escrita en la forma vectorial convencional resulta:

(2b) \frac{E}{2(1+\nu)}\Delta\mathbf{u} + \frac{E}{2(1+\nu)(1-2\nu)}\boldsymbol{\nabla}( \boldsymbol{\nabla}\cdot\mathbf{u})=\rho\ddot{\mathbf{u}}

Ondas planas

Artículo principal: Onda plana

En general una onda elástica puede ser una combinación de ondas longitudinales y de ondas transversales. Una manera simple de demostrar esto considerar la propagación de ondas planas en las que el vector de desplazamientos provocados por el paso de la onda tiene la forma \mathbf{u}=\mathbf{u}(x,t). En este caso la ecuación (2b) se reduce para una onda plana a:

\frac{\part^2u_x}{\part t^2} = E\frac{1-\nu}{\rho(1+\nu)(1-2\nu)}\frac{\part^2u_x}{\part x^2}, \qquad \frac{\part^2u_y}{\part t^2} = \frac{E}{\rho(1+\nu)} \frac{\part^2u_y}{\part x^2}, \qquad \frac{\part^2u_z}{\part t^2} = \frac{E}{\rho(1+\nu)} \frac{\part^2u_z}{\part x^2}

En las ecuaciones anteriores la componente X es una onda longitudinal que se propaga con velocidad vL mientras que la componente en las otras dos direcciones es transversal y se se propaga con velocidad vT:

\begin{matrix} u_x(x,t) = f_1\left(t-\frac{x}{v_L}\right) + g_1\left(t+\frac{x}{v_L}\right)\\ u_y(x,t) = f_2\left(t-\frac{x}{v_T}\right) + g_2\left(t+\frac{x}{v_T}\right)\\ u_z(x,t) = f_3\left(t-\frac{x}{v_T}\right) + g_3\left(t+\frac{x}{v_T}\right) \end{matrix}

Donde la velocidad de la onda longitudinal y de la onda transversal vienen dadas por:

v_L = \sqrt{\frac{E(1-\nu)}{\rho(1+\nu)(1-2\nu)}}, \qquad v_T = \sqrt{\frac{E}{2\rho(1+\nu)}}

Siendo:

E, \nu\,, el módulo de Young y el coeficiente de Poisson, respetivamente.

La siguiente tabla da las velocidades de propapagación de las ondas longitudinales y transversales en diferentes materiales:[1]

Material vL [m/s] vT [m/s]
Aluminio 6,32·103 3,07·103
Cobre 4,36·103 2,13·103
Hierro 5,80·103 3,14·103

Ondas P y S

Una descomposición más general de una onda elástica que responde a la ecuación (2b) es la descomposición de Helmholtz para campos vectoriales, en una componente longitudinal a lo largo de la dirección de propagación de la propagación y una onda transversal a la misma. Estas dos componentes se llaman usualmente componente P (onda Primaria) y componente S (onda Secundaria).

Para ver esto se define los potenciales de Helmholtz del campo de desplazamiento:

\mathbf{u} = \mathbf{u}_L + \mathbf{u}_T, \qquad \begin{cases} \mathbf{u}_L = \boldsymbol{\nabla}\phi \\ \mathbf{u}_T = \boldsymbol{\nabla}\times\boldsymbol{\psi} \end{cases}

Ondas de Rayleigh

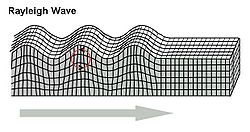
Imagen de ondas Rayleigh.

Las ondas de Rayleigh son ondas superficiales elípticas, que son una solución de la ecuación (2b), cuya amplitud disminuye exponencialmente con la profundidad. Un modelo simple de ondas de Rayleigh es que se da en un medio elástico semi-infinito, que podría representar el terreno. En términos de los potenciales elásticos, este tipo de ondas tienen la forma matemática:

\phi(x,z) = Ae^{-rz}\cos\left(\omega \left(t-\frac{x}{v_R}\right)\right), \qquad \psi(x,z) = Be^{-sz}\cos\left(\omega \left(t-\frac{x}{v_R}\right)\right)

Siendo:

A, B\,, las amplitudes de ambos potenciales.
\omega, v_R < v_T\,, la frecuencia angular y la velocidad de propagación de las ondas Rayleigh. Esta velocidad satisface la llamada condición de Rayleigh, que tiene una única solución real:
\left({2-\frac{v_R^2}{v_T^2}}\right)^2 = 4\sqrt{1-\frac{v_R^2}{v_T^2}}\sqrt{1-\frac{v_R^2}{v_L^2}}
z, x\,, son la profundidad y la distancia a lo largo de un corte vertical de terreno.
r, s\,, son dos parámetros de atenuación con la profundidad dados por:

r = \frac{\omega}{v_R}\sqrt{1-\frac{v_R^2}{v_L^2}} > 0, \qquad s = \frac{\omega}{v_R}\sqrt{1-\frac{v_R^2}{v_T^2}} > 0

v_L, v_T\,, son las velocidades de las ondas longitudinales y transversales.

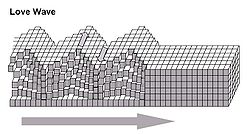
Ondas de Love

Love wave.jpg

Las ondas de Love son ondas superficiales, que requieren la existencia de una capa superficial con propiedades mecánicas ligeramente diferente de las capas más profundas.

Referencia

  1. ↑ Atkin & Fox, 1980, p. 211
  • Atkin R. J. & Fox N.: An Introduction to the Theory of Elasticity, Ed. Dover, London, 1980, ISBN 0-486-44241-1.

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Onda mecánica — Una onda mecánica es una perturbación de las propiedades mecánicas (posición, velocidad y energía de sus átomos o moléculas) que se propaga a lo largo de un material. Todas las ondas mecánicas requieren: Alguna fuente que cree la perturbación. Un …   Wikipedia Español

  • onda — ón·da s.f. 1. FO ciascuna delle masse d acqua che alternativamente si alza e si abbassa sul livello di quiete della superficie di uno specchio d acqua, spec. del mare, per effetto del vento o di altre cause: onde increspate, spumeggianti, alte,… …   Dizionario italiano

  • Onda plana — El frente de onda de una onda plana viajando en el espacio …   Wikipedia Español

  • Onda sonora — Una onda sonora es una onda longitudinal que transmite lo que se asocia con sonido. Si se propaga en un medio elástico y continuo genera una variación local de presión o densidad, que se transmite en forma de onda esférica periódica o… …   Wikipedia Español

  • Onda sísmica — Las ondas sísmicas son un tipo de onda elástica consistentes en la propagación de perturbaciones temporales del campo de tensiones que generan pequeños movimientos en un medio. Las ondas sísmicas pueden ser generadas por movimientos telúricos… …   Wikipedia Español

  • Ecuación de onda — Saltar a navegación, búsqueda La ecuación de onda es una importante ecuación diferencial parcial lineal de segundo orden que describe la propagación de una variedad de ondas, como las ondas sonoras, las ondas de luz y las ondas en el agua. Es… …   Wikipedia Español

  • Ensayos mecánicos de los materiales — Saltar a navegación, búsqueda Cuando un técnico proyecta una estructura metálica, diseña una herramienta o una máquina, define las calidades y prestaciones que tienen que tener los materiales constituyentes. Como hay muchos tipos de aceros… …   Wikipedia Español

  • assorbimento — as·sor·bi·mén·to s.m. CO 1a. l assorbire, l assorbirsi e il loro risultato: l assorbimento dell acqua da parte del terreno Sinonimi: incorporazione. 1b. fig., l accogliere, il far proprio: l assorbimento di idee altrui Sinonimi: assimilazione. 2 …   Dizionario italiano

  • fonone — fo·nó·ne s.m. TS fis. quanto di energia associato a un onda elastica Sinonimi: quanto acustico, quanto vibrazionale. {{line}} {{/line}} DATA: 1967. ETIMO: der. di fono con 3 one …   Dizionario italiano

  • microfonicità — mi·cro·fo·ni·ci·tà s.f.inv. TS elettron. 1. proprietà di determinati componenti elettrici ed elettronici che, investiti da un onda elastica, si comportano come trasduttori elettroacustici, producendo un rumore 2. disturbo che si manifesta in un… …   Dizionario italiano

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”