Polinomios de Hermite

Saltar a navegación, búsqueda

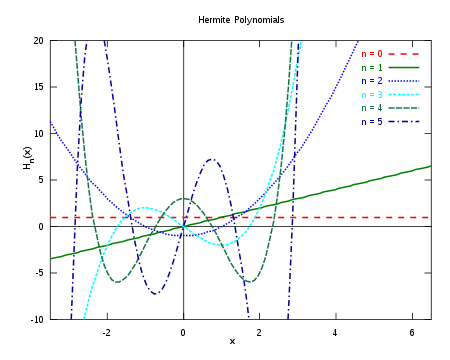
Los polinomios de Hermite son un ejemplo de polinomios ortogonales que encuentran su principal ámbito de aplicaciones en mecánica cuántica, sobre todo en el estudio del oscilador armónico unidimensional. Son nombrados así en honor de Charles Hermite.

Los cinco primeros polinomios de Hermite (probabilísticos').

Definición

Los polinomios de Hermite se definen como:

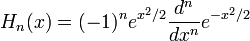
$H_n(x)=(-1)^n e^{x^2/2}\frac{d^n}{dx^n}e^{-x^2/2}\,\!$

(los "polinomios de Hermite probabilísticos") o, a veces, como (los "polinomios de Hermite físicos"):

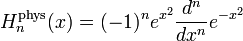
$H_n^\mathrm{phys}(x)=(-1)^n e^{x^2}\frac{d^n}{dx^n}e^{-x^2}\,\!$

Estas dos definiciones no son exáctamente equivalentes; una es un reescalado trivial de la otra:

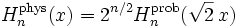$H_n^\mathrm{phys}(x) = 2^{n/2}H_n^\mathrm{prob}(\sqrt{2}\,x)\,\!$ .

Los polinomios físicos pueden expresarse como:

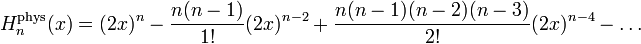
$H_n^\mathrm{phys}(x) = (2x)^n - \frac{n(n-1)}{1!}(2x)^{n-2} + \frac{n(n-1)(n-2)(n-3)}{2!}(2x)^{n-4} - \dots$

Propiedades

Ortogonalidad

H_n(x) es un polinomio de grado n, con n = 0, 1, 2, 3, .... Estos polinomios son ortogonales con respecto de la función peso (medida)

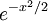$e^{-x^2/2}\,\!$ (probabilista)

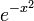$e^{-x^2}\,\!$ (física)

es decir

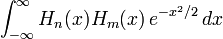
$\int_{-\infty}^\infty H_n(x)H_m(x)\,e^{-x^2/2}\,dx$

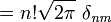$=n!\sqrt{2\pi}~\delta_{\mathit{nm}}$ (probabilista)

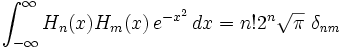$\int_{-\infty}^\infty H_n(x)H_m(x)\,e^{-x^2}\,dx={n!2^n}{\sqrt{\pi}}~\delta_{\mathit{nm}}$ (física)

donde δ_ij es la delta de Kronecker, que vale la unidad cuando n = m y cero en otro caso. Los polinomios probabilísticos son ortogonales con respecto a la función de densidad de probabilidad normal.

Función generadora

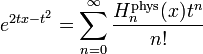
$e^{2tx-t^2} = \sum_{n=0}^\infty \frac{H_n^\mathrm{phys}(x)t^n}{n!}$

Fórmulas de recurrencia

Los polinomios de Hermite (en su forma "física") satisfacen la siguiente relaciones de recurrencia:

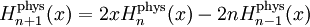
$H_{n+1}^\mathrm{phys}(x) = 2xH_{n}^\mathrm{phys}(x)-2nH_{n-1}^\mathrm{phys}(x)$

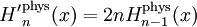
${H'}_{n}^\mathrm{phys}(x) = 2nH_{n-1}^\mathrm{phys}(x)$

Descomposición en serie de funciones

Toda función f continua puede expresarse como serie infinita en términos de polinomios de Hermite:

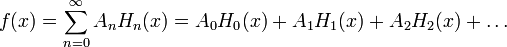
$f(x) = \sum_{n=0}^\infty A_n H_n(x) = A_0H_0(x) +A_1H_1(x) +A_2H_2(x) +\ldots$

Donde las constantes de la anterior serie vienene dados por:

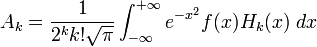
$A_k = \frac{1}{2^kk!\sqrt{\pi}} \int_{-\infty}^{+\infty} e^{-x^2}f(x)H_k(x)\ dx$

Otros resultados

$H_n(-x)=(-1)^nH_n(x)\,$

$H_{2n-1}(0)=0\,$

$H_{2n}^\mathrm{phys}(0) = (-1)^n2^n(1\cdot3\cdot5\cdot\dots\cdot(2n-1)$

Ecuación diferencial de Hermite

Los polinomios de Hermite son soluciones de la ecuación diferencial de Hermite:^[1]

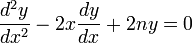
$\frac{d^2y}{dx^2}-2x\frac{dy}{dx}+2ny = 0$

que en forma canónica puede escribirse como:

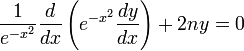
$\frac{1}{e^{-x^2}}\frac{d}{dx}\left(e^{-x^2}\frac{dy}{dx}\right)+2ny = 0$

Referencia

↑ Spiegel & Abellanas, 1992, p.158.

Spiegel, Murray R.; Abellanas, Lorenzo (1992). McGraw-Hill (ed.). Fórmulas y tablas de matemática aplicada. ISBN 84-7615-197-7.

Obtenido de "Polinomios de Hermite"

Categoría: Funciones especiales

Wikimedia foundation. 2010.

Игры ⚽ Нужно сделать НИР?

Mira otros diccionarios:

Polinomios de Laguerre — Saltar a navegación, búsqueda Los polinomios de Laguerre son una familia de polinomios ortogonales, llamados así en honor de Edmond Laguerre, surgen al examinar las soluciones a la ecuación diferencial: Desarrollando y en serie de potencias se… … Wikipedia Español
Polinomios ortogonales — Saltar a navegación, búsqueda Los polinomios ortogonales son conjuntos de polinomios que forman una base ortogonal son importantes porque aparecen en la teoría de ecuaciones diferenciales, muy especialmente en la teoría de Sturm Liouville, la… … Wikipedia Español
Polinomios de Chebyshov — En matemática, los polinomios de Chebyshov, nombrados en honor a Pafnuti Chebyshov, son una familia de polinomios ortogonales que están relacionados con la fórmula de De Moivre y son definidos de forma recursiva con facilidad, tal como ocurre con … Wikipedia Español
polinomios ortogonales — Sistema de polinomios que son mutuamente ortogonales (ortogonalidad es el análogo de perpendicularidad en mayores dimensiones), útil en la solución de ecuaciones diferenciales de la física e ingeniería. El estudio de tales sistemas empezó con… … Enciclopedia Universal
Polinomios de Legendre — Saltar a navegación, búsqueda En matemáticas al resolver la formula de Rodrigues, las Funciones de Legendre son las soluciones a las Ecuaciones Diferenciales de Legendre: llamadas así por el matemático francés Adrien Marie Legendre. Estas… … Wikipedia Español
Hermite — Hermite, polinomios de … Enciclopedia Universal
Hermite, polinomios de — ► MATEMÁTICAS Familia de polinomios ortogonales, atribuidos a Ch. Hermite (1822 1901), que se obtiene al variarnombre en la fórmula ; Hn (x) es el polinomio de Hermite de grado nombre … Enciclopedia Universal
Charles Hermite — (c. 1887). Nacimiento 24 de diciembre de 1822 [[Archivo:{{{bandera alias 1638}}}|20x20px|border … Wikipedia Español
Charles Hermite — (Dieuze, Francia, 24 de diciembre de 1822 París, 14 de enero de 1901) fue un Matemático francés que investigó en el campo de la teooría de los números, sobre las formas cuadráticas, polinomios ortogonales y funciones elípticas, y en el álgebra.… … Enciclopedia Universal
Anexo:Matemáticos importantes — En esta lista de matemáticos importantes se presenta una selección de matemáticos desde la antigüedad hasta el presente. La selección se orienta por los aportes científicos, utilizando como criterio para definir el grado de notoriedad la atención … Wikipedia Español

Los diccionarios y las enciclopedias sobre el Académico

Polinomios de Hermite

Polinomios de Hermite

Contenido

Definición