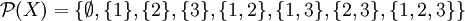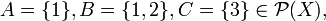Relación de orden

Relación de orden

Relación de orden

Sea A un conjunto dado no vacío y R una relación binaria definida en A, entonces decimos que R es una relación de orden si cumple las siguientes propiedades:

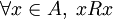  1. Reflexividad: Todo elemento de A está relacionado consigo mismo. Es decir, \forall x\in A, \; xRx.
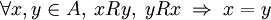
  2. Antisimetría: Si dos elementos de A se relacionan entre sí, entonces ellos son iguales. Es decir, \forall x,y\in A, \; xRy, \; yRx \; \Rightarrow \; x=y
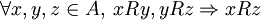
  3. Transitividad: Si un elemento de A está relacionado con otro, y ese otro a su vez se relaciona con un tercero, entonces el primero estará relacionado también con este último. Es decir, \forall x,y,z\in A, \; xRy , yRz \Rightarrow xRz

Una relación de orden R sobre un conjunto A puede denotarse con el par ordenado (A,\le).

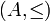Contenido

Relación de orden total

Sea A un conjunto dado, 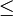\le es una relación de orden total si y solo si todos los elementos de A se relacionan entre sí, es decir,

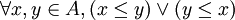\forall x,y\in A, (x\le y) \vee (y\le x).

  • Ejemplo 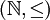(\mathbb{N},\le) es totalmente ordenado. En efecto, es:
    • Reflexivo: 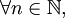\forall n\in\mathbb{N}, entonces 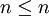n\le n (porque por definición, n=n\,)
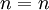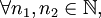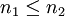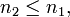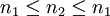
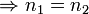
    • Antisimétrico: \forall n_1, n_2\in\mathbb{N}, si \; \; n_1\le n_2\; \; y \; \; n_2\le n_1,\; \; entonces n_1\le n_2\le n_1 \Rightarrow n_1=n_2
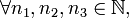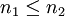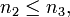    • Transitivo: \forall n_1,n_2,n_3\in\mathbb{N}, si \; \; n_1\le n_2\; \; y \; \; n_2\le n_3,\; \; entonces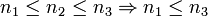 n_1\le n_2\le n_3 \Rightarrow n_1\le n_3

Relación de orden parcial

Sea A un conjunto dado, 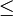\le es una relación de orden parcial si y solo si al menos un par de elementos de A se relacionan entre sí, es decir,

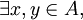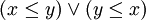\exists x,y\in A, tal que (x\le y) \vee (y\le x).

\mathcal{P}(X)=\{ \emptyset, \{1\}, \{2\}, \{3\}, \{1, 2\}, \{1, 3\}, \{2, 3\}, \{1, 2, 3\} \}

Entonces 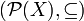(\mathcal{P}(X), \subseteq) es parcialmente ordenado, pues sean

A=\{1\}, B=\{1,2\}, C=\{3\}\in\mathcal{P}(X),
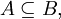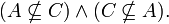
A\subseteq B, pero (A\nsubseteq C) \wedge (C\nsubseteq A).

Nótese que las relaciones de orden total son un caso particular de las relaciones de orden parcial.

Relación de orden densa

Véase también: Conjunto denso

Una relación de orden parcial ≤ sobre un conjunto X se dice densa (o densa-en -sí-misma) si, para todo x e y en X tales que x < y (x ≤ y y x ≠ y), existe otro z en X tal que x < z < y.

  • Ejemplo 1: Los números racionales con la ordenación habitual son un conjunto densamente ordenado, al igual que los números reales. Si q1 < q2 entonces tenemos que q3 := (q1+q2)/2 satisface que: q1 < q3 < q2.
  • Ejemplo 2: Los números enteros por otro lado con la ordenación habitual no son un cojunto densamente ordenado ya que entre un número entero y su siguiente no existe un número intermedio.

Véase también

Esquema de temas relacionados

Teoría del orden
Bien ordenado
Orden total
Parcialmente ordenado
Preordenado
Relación reflexiva
Relación transitiva
Relación antisimétrica
Relación total
Orden bien fundamentado
Obtenido de "Relaci%C3%B3n de orden"

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Orden bien fundamentado — Saltar a navegación, búsqueda En matemáticas, una relación binaria, R, es bien fundamentada (o bienfundamentada) en una clase X si y sólo si todo subconjunto no vacío de X tiene un elemento R mínimo; esto es, para todo subconjunto no vacío S de X …   Wikipedia Español

  • Orden (desambiguación) — Orden puede adqurir varios significados en diferentes disciplinas. Puede referirse a: Contenido 1 Teoría de sistemas 2 Criterios de ordenación 3 Significados en diferentes ciencias 3.1 …   Wikipedia Español

  • Relación — Saltar a navegación, búsqueda El concepto relación puede referirse a muy distintos ámbitos: Contenido 1 En el sentido de relato 1.1 Folclore 1.2 Literatura …   Wikipedia Español

  • Relación binaria — Saltar a navegación, búsqueda En matemáticas, una relación binaria es una relación matemática R entre los elementos de dos conjuntos A y B. Una relación de este tipo se puede representar mediante pares ordenados, : Las dos propo …   Wikipedia Español

  • Relación matemática — Saltar a navegación, búsqueda Una relación , de los conjuntos es un subconjunto del producto cartesiano Una Relación binaria es una relación entre dos conjuntos. El concepto de relación implica la idea de enumeración, de algunos de los elementos …   Wikipedia Español

  • Orden — (Del lat. ordo, inis.) ► sustantivo masculino 1 Colocación cuidadosa de un conjunto de cosas, asignando a cada una un lugar o posición determinada: ■ quiero que todo esté en orden. ANTÓNIMO desorden 2 Disposición regular de un conjunto de cosas o …   Enciclopedia Universal

  • Relación de equivalencia — Una relación de equivalencia sobre K es una relación binaria Relación de equivalencia que cumple las siguientes propiedades: ● Es reflexiva: ∀a ∈ K, a Relación de equivalencia a. ● Es simétrica: a Relación de equivalencia b ⇒ b Relación de equiva …   Enciclopedia Universal

  • Orden lexicográfico — El orden lexicográfico es una relación de orden que se utiliza para ordenar producto cartesiano de conjuntos ordenados. Es conocido principalmente por su aplicación a cadenas de caracteres, por ejemplo en diccionarios o en la guía telefónica.… …   Wikipedia Español

  • Orden vectorial — El orden vectorial es la relación de orden utilizada para ordenar vectores. Sean y los conjuntos y ordenados, respectivamente, mediante las relaciones de orden y , entonces el orden vectorial …   Wikipedia Español

  • orden — Economía. Instrucción para actuar dada por una persona con poder suficiente (de embarque, de producción, etc. ). Disposición metódica de acuerdo a una relación deseada. orden de comparecencia orden de detención Ver: a la orden …   Diccionario de Economía Alkona

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”