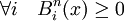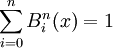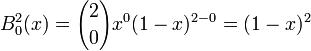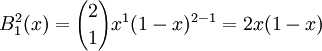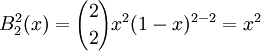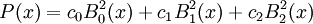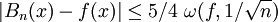- Polinomio de Bernstein
-
Polinomio de Bernstein
Los polinomios de Bernstein o polinomios en la base de Bernstein son una particular clase de polinomios (en el campo de los números reales), tales polinomios son utilizados dentro del ámbito del análisis numérico. El nombre hace referencia al matemático ucraniano Sergei Natanovich Bernstein.
El algoritmo de evaluación más numéricamente estable es el de de Casteljau.
Contenido
Definición
Un polinomio de Bernstein P(x) de grado n procede de la fórmula:
donde los
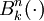 son elementos de la base de los polinomios de Bernstein, definidos de:
son elementos de la base de los polinomios de Bernstein, definidos de:o, más en general:
(aquí
 es el coeficiente binomial).
es el coeficiente binomial).Propiedades
Los polinomios de base de Bernstein forman una combinación convexa, en efecto, resulta que:
Escala y traslación
La modificación por escala y traslación de intervalo no influye sobre los coeficientes del polinomio en cuestión.
Ejemplo
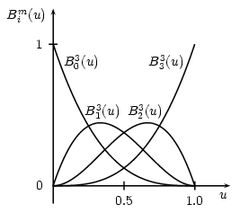
Archivo:Basi Bernstein grado 2.pngRepresentación de la base de Bernstein para polinomios de grado 2.En el caso de un polinomio de grado 2 la base en [0,1] está compuesta de:
Un polinomio expresado en esta base tendría entonces la forma:
Descripción
Para un grado m, existen m+1 polinomios de Bernstein
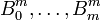 definidos sobre el intervalo [0,1], por
definidos sobre el intervalo [0,1], por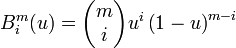 ,
,
donde las
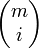 son los coeficientes binomiales.
son los coeficientes binomiales.Estos polinomios presentan cuatro propiedades importantes :
- Partición de la unidad :
![\qquad \sum_{i=0}^m B_i^m(u) = 1, \qquad \forall u \in [0,1]](/pictures/eswiki/52/4f793153ea646b8540577aadf07c4e57.png)
- Positividad :
![B_i^m(u) \geq 0, \qquad \forall u \in [0,1], \forall i \in 0 \dots m](/pictures/eswiki/97/a76d85c6cfc54ce4dc4325c08e1376d5.png)
- Simetría :
![B_i^m(u) = B_{m-i}^m(1-u), \qquad \forall u \in [0,1], \forall i \in 0 \dots m](/pictures/eswiki/57/9d1089543daf80d286e35839c998dfe6.png)
- Fórmula de recurrencia :
![B_i^m(u) =
\begin{cases}
(1-u)B_i^{m-1}(u),& i = 0\\
(1-u)B_i^{m-1}(u) + u B_{i-1}^{m-1}(u),&\forall i \in 1 \dots m-1\\
uB_{i-1}^{m-1}(u),& i = m
\end{cases}
, \qquad \forall u \in [0,1]](/pictures/eswiki/50/2b11f69a8ed42363217d3254666c8fb2.png) .
.
Se ha de notar la gran semejanza de estos polinomios con la ley binomial.
Aplicaciones
Los polinomios de Bernstein son utilizados para demostrar el teorema de aproximación de Weierstrass y por esto son también utilizados para efectuar aproximaciones e interpolaciones de funciones como, por ejemplo, la curva de Beziér, así como para la estimación de las funciones de densidad de probabilidad:
Para n que tiende al infinito, el polinomio converge uniformamente hacia la función f (x), o seadonde
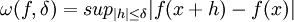 , llamado módulo de continuidad.
, llamado módulo de continuidad.
Véase también
- Algoritmo de de Casteljau
- Curva de Beziér
- Aproximación de Bernstein, permite aproximar uniformemente funciones continuas.
Categoría: Polinomios
Wikimedia foundation. 2010.

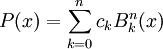
![B^n_i (x) = {n \choose i} x^i (1 - x)^{n - i} \quad \textrm{si } \quad x \in [0,1];](/pictures/eswiki/51/35eebe02760c033c668ecd061c0f915a.png)
![B^n_i (x) = {n \choose i} {(b-x)^{n-i}(x-a)^i \over (b-a)^n} \quad \textrm{si}\quad x \in [a,b];](/pictures/eswiki/57/9f70c6c4f359d1e4b39ffb594792688d.png)