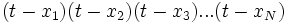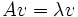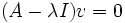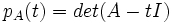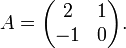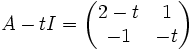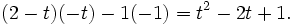En álgebra lineal, se asocia un polinomio a cada matriz cuadrada llamado polinomio característico. Dicho polinomio contiene una gran cantidad de información sobre la matriz, los más significativos son los valores propios, su determinante y su traza.

Contenido 1 Motivación 2 Definición formal 3 Ejemplos 4 Propiedades

Motivación

Dada una matriz cuadrada A, queremos encontrar un polinomio cuyas raíces son precisamente los valores propios de A. Para una matriz diagonal A, el polinomio característico es fácil de definir: si los elementos de la diagonal son x_i para i = 1..N, el polinomio característico en la indeterminada t es

El polinomio tiene esta forma ya que los elementos de la diagonal de una matriz diagonal coinciden con sus valores propios.

Para una matriz A genérica, se puede proceder de la siguiente forma: Si λ es un valor propio de A, entonces existe un vector propio v≠0 tal que

o

(donde I es la matriz identidad). Como que v es no nulo, la matriz λI − A es singular, que a su vez significa que su determinante es 0. Acabamos de ver que las raíces de la función det(A-t I) son los valores propios de A. Como que dicha función es un polinomio en t, ya está.

Definición formal

Sea K un cuerpo (podemos imaginar K como el cuerpo de los reales o de los complejos) y una matriz cuadrada A n-dimensional sobre K. El polinomio característico de A, denotado por p_A(t), es el polinomio definido por

donde I denota la matriz identidad n-por-n. Algunos autores definen el polinomio característico como det(t I-A); la diferencia es inmaterial puesto que los dos polinomios únicamente se diferencian por su signo.

Ejemplos

Supongamos que queremos encontrar el polinomio característico de la matriz

Debemos calcular el determinante de

dicho determinante es

Finalmente hemos obtenido el polinomio característico de A.

Propiedades

El polinomio p_A(t) es mónico (su coeficiente dominante es 1) y de grado n. El hecho más importante sobre el polinomio característico ya fue mencionado en el parágrafo de motivación: los valores propios de A son precisamente las raíces de p_A(t). El coeficiente constante p_A(0) es igual a (−1)ⁿ veces el determinante de A, y el coeficiente de t ^{n − 1} es igual a -tr(A), la traza de A. Para una matriz A de 2×2, el polinomio característico se puede expresar como: t ² − tr(A)t + det(A).

Todos los polinomios reales de grado impar tienen al menos un número real como raíz, así que para todo n impar, toda matriz real tiene al menos un valor propio real. La mayoría de los polinomios reales de grado par no tienen raíces reales, pero el teorema fundamental del álgebra dice que todo polinomio de grado n tiene n raíces complejas, contadas con sus multiplicidades. Las raíces no reales de polinomios reales, por tanto valores propios no reales, aparecen en pares conjugados.

El teorema de Cayley-Hamilton dice que si reemplazamos t por A en la expresión de p_A(t) obtenemos la matriz nula: p_A(A) = 0. Es decir, toda matriz satisface su propio polinomio característico. Como consecuencia de este hecho, se puede demostrar que el polinomio mínimo de A divide el polinomio característico de A.

Dos matrices semejantes tienen el mismo polinomio característico. El recíproco no es cierto en general: dos matrices con el mismo polinomio característico no tienen porque ser semejantes.

La matriz A y su transpuesta tienen el mismo polinomio característico. A es semejante a una matriz triangular si y solo si su polinomio característico puede ser completamente factorizado en factores lineales sobre K. De hecho, A es incluso semejante a una matriz en forma canónica de Jordan.