- Polinomio ciclotómico
-
Polinomio ciclotómico
Se denomina polinomio ciclotómico de orden n y se denota como Φn al polinomio unitario cuyas raíces son todas las raíces primitivas de orden n de la unidad, es decir, que verifican zn = 1 .
Se suele tomar las raíces en el cuerpo de los complejos, (otras extensiones del cuerpo de los reales serían posibles), pero carece de consecuencia sobre los polinomios ciclotómicos, cuyos coeficientes son siempre enteros.
El grado de Φn es dado por la función φ de Euler, y es lógicamente inferior o igual a n.
Existe un isomorfismo natural entre el conjunto Un={1, ω ω²,... ωn-1 } de las raíces de orden n de la unidad, que es un grupo, y el grupo cíclico Z/nZ= Zn (provisto de la ley «+» únicamente):
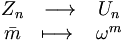
Las raíces primitivas son los generadores del grupo Un y corresponden por este isomorfismo a los de Z/nZ. Por lo tanto son de la forma ωr, con 0 ≤ r < n, r coprimo con n, y
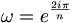 .
.Luego : 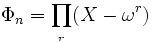
Dos ejemplos:
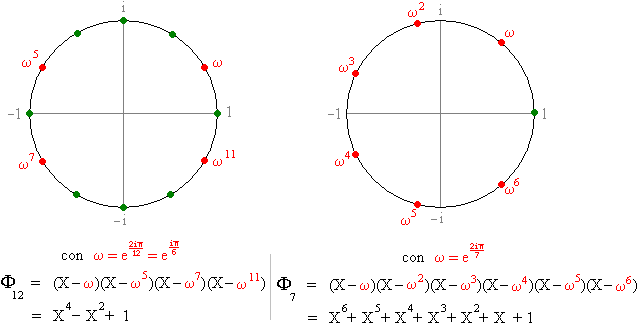
En rojo están las raíces primitivas, en verde las demás.
Sin embargo, no es está fórmula la que se emplea para calcular los Φn, sino la siguiente: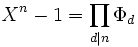
demostrada aquí, y que se puede escribir así: 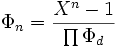
con d \ n, 0 < d < n en el producto. lo que permite encontrar los polinomios por inducción :
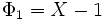
, aplicando la definición. Luego: X+1 </math>
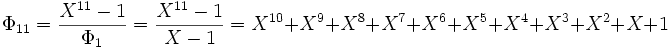
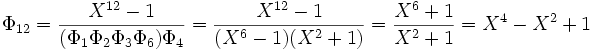
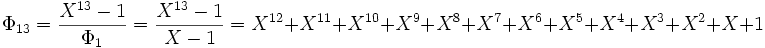
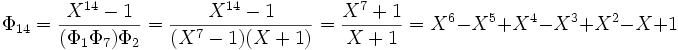
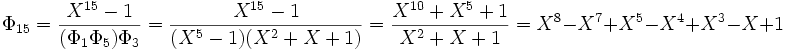
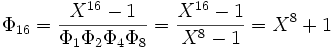
Los coeficientes son siempre enteros porque se divide un polinomio de Z[X] unitario por otros que lo son también (lo que se demuestra por inducción otra vez). En este caso, la división euclidiana consiste es una sucesión de sustracciones, sin ninguna división entre números.
Mirando mejor los polinómios, uno tiene la impresión que los coeficientes sólo pueden ser -1; O ó 1. Pues no es el caso, aunque hay que indagar bastante profundo para hallar el primer contraejemplo: con 105 = 3 × 5 × 7, el primer producto de tres primos impares, se obtiene:
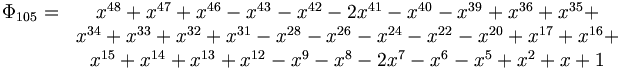
Se observan dos coeficientes "2", en x41 y x7.
Se nota que si n es primo, entonces : 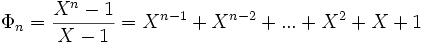
Esto se deduce de la fórmula que da la inducción (con Φ1 = X - 1), pero también se puede demostrar observando que todas las raíces de orden n salvo z = 1 son primitivas, por lo que hay que dividir Xn - 1 por X - 1.
En algunos contextos se necesita trabajar en extensiones del cuerpo que contengan raíces de la unidad, para poder factorizar polinomios por ejemplo, pero que no contengan todos los complejos. La idea es prescindir lo más posible de los irracionales (y de los complejos con componentes irracionales), que son muy difíciles de programar (un irracional cualquiera vienen dado a priori por una infinidad aleatoria de dígitos, y esto no cabe en un ordenador).
La menor extensión de Q que contenga las raíces de orden n de 1 es Q(ω) donde ω es una raíz primitiva de orden n (por ejemplo :
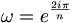 ).
).Como ω es una raíz Φn que es un polinomio irreductible sobre Q, entonces Q(ω) es el cuerpo de ruptura del polinomio Φn, y se llama cuerpo ciclotómico de orden n, se denota a menudo Fn y se define como el cociente de Q[X] por el ideal generado por Φn:
![F_n = Q(e^{\frac {2i \pi} n }) = Q[X]/ (\Phi_n)](/pictures/eswiki/51/3ff2f4d6c7e86c97134889c63d6ed574.png)
Ejemplos:
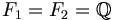
![F_3 = \mathbb{Q}[X]/ (X^2+X+1)](/pictures/eswiki/102/f828e2563608fc8cf658b73da0692416.png)
es el conjunto de los polinomios en la variable 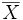
que verifica 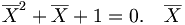
tiene el papel de 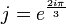
que también verifica j² + j + 1 =0. ![F_4 = \mathbb{Q}[X]/ (X^2+1)](/pictures/eswiki/53/5cb329da9fc3a378aaf86d451ee31aa0.png)
es el conjunto de los polinomios en la variable 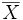
que verifica 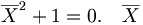
tiene lógicamente el papel de i, con i² = -1.
Categoría: Polinomios
Wikimedia foundation. 2010.
