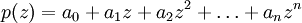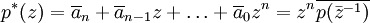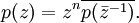Polinomio recíproco

Polinomio recíproco

Polinomio recíproco

En matemáticas, para un polinomio p con coeficientes complejos,

p(z) = a_0 + a_1z + a_2z^2 + \ldots + a_nz^n \,\!

se define el polinomio recíproco, p*

p^*(z) = \overline{a}_n + \overline{a}_{n-1}z + \ldots + \overline{a}_0z^n = z^n\overline{p(\bar{z}^{-1})}

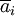donde \overline{a}_i denota el conjugado complejo de a_i \,\!.

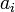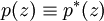Un polinomio se dice que es autorrecíproco si p(z) \equiv p^{*}(z).

Si los coeficientes ai son reales, entonces esto se reduce a ai = an−i. En este caso, se dice que p es un polinomio palindrómico.

Si p(z) es el polinomio mínimo de z0 con |z0| = 1, y p(z) tiene coeficientes reales, entonces p(z) es autorrecíproco. Esto es así porque

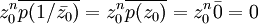z_0^n\overline{p(1/\bar{z_0})} = z_0^n\overline{p(z_0)} = z_0^n\bar{0} = 0.

Por tanto, z0 es una raíz del polinomio 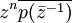z^n\overline{p(\bar{z}^{-1})}, que tiene grado n. Sin embargo, el polinomio mínimo es único, por tanto

p(z) = z^n\overline{p(\bar{z}^{-1})}.

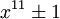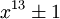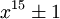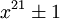Una consecuencia de esto es que los polinomios ciclotómicos Φn son autorrecíprocos para n > 1. Este resultado se utiliza en la criba especial del cuerpo de números para permitir que números de la forma x^{11} \pm 1, x^{13} \pm 1, x^{15} \pm 1 y x^{21} \pm 1 puedan ser factorizados tomando partido de los factores algebraicos mediante el uso de polinomios de grado 5, 6, 4 y 6 respectivamente. Nótese que el φ de los exponentes es 10, 12, 8 and 12.

Véase también

  • Transformada de Schur

Enlaces externos

Obtenido de "Polinomio rec%C3%ADproco"

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Polinomio característico — Saltar a navegación, búsqueda En álgebra lineal, se asocia un polinomio a cada matriz cuadrada llamado polinomio característico. Dicho polinomio contiene una gran cantidad de información sobre la matriz, los más significativos son los valores… …   Wikipedia Español

  • Vector propio y valor propio — Fig. 1. En esta transformación de la Mona Lisa, la imagen se ha deformado de tal forma que su eje vertical no ha cambiado. (nota: se han recortado las esquinas en la imagen de la derecha) …   Wikipedia Español

  • Problema de Galois inverso — Problemas no resueltos de la matemática: Todo polinomio con coeficientes racionales lleva asociado un grupo de Galois, pero ¿es cierto que todo grupo finito es grupo de Galois de algún polinomio? En teoría de Galois, el problema de Galois inverso …   Wikipedia Español

  • Álgebra elemental — El álgebra elemental es una fundamental y relativamente básica forma de álgebra enseñada a los estudiantes que se presumen tienen poco o nada de conocimiento formal de las matemáticas más allá de la aritmética. Mientras que en aritmética solo… …   Wikipedia Español

  • Ajuste de curvas — El ajuste de curvas consiste en encontrar una curva que contenga una serie de puntos y que posiblemente cumpla una serie de restricciones adicionales. Esta sección es una introducción tanto a la interpolación (cuando se espera un ajuste exacto a… …   Wikipedia Español

  • Teorema de Wilson — En matemáticas, el teorema de Wilson es un teorema clásico relacionado con la divisibilidad. Se enuncia de la siguiente manera: Si p es un número primo, entonces (p − 1)!+1 ≡ 0 (mod p) John Wilson El recíproco también es cierto, por lo que puede… …   Wikipedia Español

  • Número de Salem — En matemáticas, un entero algebraico real es un número de Salem si todas sus raíces conjugadas tienen valor absoluto menor o igual que 1, y al menos una de ellas tiene valor absoluto exactamente igual a 1. Los números de Salem, llamados así en… …   Wikipedia Español

  • Derivada — La derivada de la función en el punto marcado equivale a la pendiente de la recta tangente (la gráfica de la función está dibujada en negro; la tangente a la curva está dibujada en rojo). En matemáticas, la derivada de una función es una medida… …   Wikipedia Español

  • Potencia — (Del lat. potentia.) ► sustantivo femenino 1 Capacidad para hacer una cosa: ■ potencia muscular; potencia auditiva; potencia militar de un estado. SINÓNIMO poder ANTÓNIMO impotencia 2 Persona, entidad o nación que tiene gran poder sobre las demás …   Enciclopedia Universal

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”