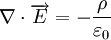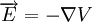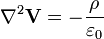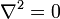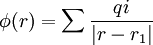En el estudio de las macromoléculas es posible hacer uso de ecuaciones utilizadas habitualmente en la dinámica de fluidos o en el electromagnetismo; una de estas es la ecuación de Poisson, que es posible obtener a partir de la ley de Gauss en forma diferencial:

con:

Reemplazando, se obtiene:

la cual es la ecuación de Poisson, si se toma en una región del campo donde la densidad de carga ρ es cero:

cuya ecuación es la ecuación de Laplace.

Una de las características del operador laplaciano es ser invariante, por que es el resultado de dos operaciones sucesivas invariantes. Por ejemplo, el laplaciano de un potencial electrostático es cero en regiones donde hay carga espacial cero. Así, el problema general se remonta a encontrar el potencial electrostático V correspondiente a una distribución de carga dada y encontrar una solución de la ecuación de Laplace o de Poisson que satisfaga las condiciones de contorno.

Condiciones de contorno

• Potencial: en la frontera entre 2 medios diferentes el potencial debe ser continuo. Una discontinuidad implicaría una intensidad infinitamente grande de campo eléctrico, lo cual es imposible en la física. El potencial debe ser cero en el infinito si la distribución de carga está extendida de manera finita, y debe ser constante a través de algún conductor en todo el tiempo que las cargas estén en reposo.

• Momento dipolar inducido: moléculas polarizadas o con un diminuto desplazamiento de las cargas positivas (+) y negativas (-)

• Equilibrio de polarización: debe existir alineación neta.

Los modelos electrostáticos asumidos para estudiar las macromoléculas están basados en la ecuación de Poisson. Las dificultades que esto implican tienen que ver con el hecho de que, teniendo los modelos macromoleculares, se requieren los métodos para aplicar la ecuación de Poisson. Si las cargas se representan explícitamente como formas puntuales, y sus interaccione se efectúan en el espacio libre, se puede aplicar como solución la ley de Coulomb:

donde la sumatoria se efectúa sobre todas las i, el término r₁ es la posición y el qi la magnitud de la i+n cargas puntuales.

En otros casos puede suceder que si la distribución de carga que genera el potencial está presente en un medio complejo, es posible usar promedios espaciales para cuantificar la respuesta del medio a los campos generados por la distribución de carga.

Si el dieléctrico varía en el espacio, entonces la ecuación de Poisson toma la forma:

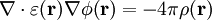
Puesto que tal distribución de carga puede estar en un medio complejo se puede promediar la respuesta del medio ante ese campo eléctrico por medio de los momentos dipolares.

Véase también

• Macromolécula
• Ecuación de Poisson