Radio de convergencia

Radio de convergencia: Radio de convergencia

Saltar a navegación, búsqueda

En matemáticas, el radio de convergencia de una serie según el teorema de Cauchy-Hadamard viene dado por la expresión:

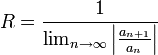
$R = \frac{1}{\lim_{n \to \infty} \left | \frac{a_{n+1}}{a_n} \right |}$

Contenido

1 Definición

2 Ejemplos

2.1 Radio de convergencia finito puys

2.2 Distancia a la singularidad

2.3 Radio de convergencia infinito

3 Véase también

Definición

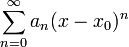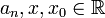Si nos limitamos al conjunto de los números reales, una serie de la forma $\sum_{n=0}^\infty a_n(x-x_0)^n$ , con $a_n,x,x_0\in\mathbb{R}$ , recibe el nombre de serie de potencias centrada en $x 0$ . La serie converge absolutamente para un conjunto de valores de $x$ que verifica que $| x - x 0 | < r$ , donde r es un número real llamado radio de convergencia de la serie. Esta converge, pues, al menos, para los valores de $x$ pertenecientes al intervalo $(x 0 - r,$ $x 0 + r)$ , ya que la convergencia para los extremos de este ha de estudiarse aparte, por lo que el intervalo real de convergencia puede ser también semiabierto o cerrado. Si la serie converge solo para $x 0$ , $r = 0$ . Si lo hace para cualquier valor de $x$ , $r =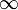$ $\infty \,\!$

Ejemplos

Mostraremos el radio de convergencia de algunos desarrollos en series de potencias con sus respectivos radios de convergencia sin justificar porqué el radio de convergencia es el dado.

Radio de convergencia finito puys

La función $1 / (1 - x)$ en su desarrollo con centro 0, o sea, en series de potencia $x - x 0 = x - 0 = x$ , tiene el siguiente aspecto:

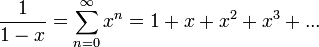$\frac{1}{1-x}=\sum_{n=0}^\infty x^n=1+x+x^2+x^3+...$ .

(para el cálculo de la serie vea serie de Taylor). Su radio de convergencia es $r = 1$ . Eso significa que para calcular si tomo cualquier valor cuya distancia al $x 0 = 0$ es menor que $r = 1$ , por ejemplo el $x = 0.25$ , entonces al remplazarlo en la serie el resultado de calcular la serie será el mismo que remplazarlo en la función, de hecho

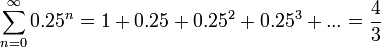$\sum_{n=0}^\infty 0.25^n=1+0.25+0.25^2+0.25^3+...=\frac{4}{3}$ .

(la cuenta se puede hacer por serie de potencia). Y por otro lado

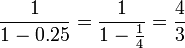$\frac{1}{1-0.25}=\frac{1}{1-\frac{1}{4}}=\frac{4}{3}$ .

Pero si tomamos un elemento fuera del radio de convergencia, por ejemplo el $x = 2$ , los más probable es que al remplazarlo en la serie, ésta diverja (por eso el nombre de radio de convergencia). Efectivamente:

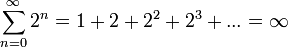$\sum_{n=0}^\infty 2^n=1+2+2^2+2^3+...=\infty$ .

Distancia a la singularidad

El cálculo del radio de convergencia no es simple. Veamos una función con dos desarrollos en serie con distintos centros y analicemos sus radios de convergencia. La misma función $1 / (1 - x)$ en su desarrollo con centro $x 0 = 2$ tiene al forma:

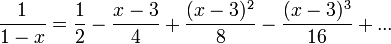$\frac{1}{1-x}=\frac{1}{2}-\frac{x-3}{4}+\frac{(x-3)^2}{8}-\frac{(x-3)^3}{16}+...$ .

Pero en este caso su radio de convergencia es $r = 2$ . Notemos que la función $1 / (1 - x)$ tiene una singularidad en el 1; y que en los dos caso anteriores el radio de convergencia concide con la ditancia cel centro a la singularidad: $| 0 - 1 | = 1$ y $| 3 - 1 | = 2$ . Esto será siempre verdadero para esta función pero no puede generalizarse, como veremos en el siguiente ejemplo:

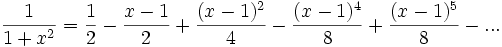$\frac{1}{1+x^2}=\frac{1}{2}-\frac{x-1}{2}+\frac{(x-1)^2}{4}-\frac{(x-1)^4}{8}+\frac{(x-1)^5}{8}-...$ .fgfhfgh

Como no hay singularidades reales podría suponerse que el radio es infinito, sin embargo su radio de convergencia es 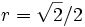$r=\sqrt{2}/2$ . Este radio parece caprichoso pero tiene que ver con el hecho de que pasando la función a dominio complejo, existe una singularidad en el denominador.La serie

Radio de convergencia infinito

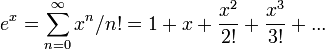Por ejempo, la función $e x$ puede desarrollarse en series de potencia de $x - 0 = x$ , de hecho $e^{x}=\sum_{n=0}^\infty x^n/n!=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+...$ .

y esto vale para todo real $x$ por eso el radio de convergencia será infinito.

Véase también

Serie matemática

Serie de Laurent

Obtenido de "Radio de convergencia"

Categoría: Series matemáticas

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

Radio Montaillou Pyrénées — Propriétaire Radio Télé Montaillou Slogan « La radio des vallées » Langue Français Pays … Wikipédia en Français
Convergéncia occitana — Convergence occitane Convergence occitane (Convergéncia Occitana en occitan) est un collectif associatif qui rassemble soixante et onze associations engagées pour la culture occitane dans la région de Toulouse principalement. Elle fut créée le 20 … Wikipédia en Français
Serie hipergeométrica — En matemáticas, una serie hipergeométrica es una serie de potencias donde el k ésimo coeficiente de la serie es una función racional de k. Si la serie converge, define una función hipergeométrica cuyo dominio es algún subconjunto de los números… … Wikipedia Español
Extensión analítica — En análisis complejo que es una rama de las matemáticas, una extensión analítica (o continuación analítica) es una técnica para extender el dominio de definición de una dada función analítica. Una extensión analítica por lo general tiene éxito en … Wikipedia Español
Teorema de Cauchy-Hadamard — En matemática, el Teorema de Cauchy Hadamard, llamado así por los matemáticos franceses Augustin Louis Cauchy y Jacques Hadamard, estableciendo el radio de convergencia de una serie de potencias que aproxima una función en torno de un punto a.… … Wikipedia Español
Fracción continua de Gauss — Saltar a navegación, búsqueda En análisis complejo la fracción continua de Gauss es un caso particular de fracción continua generalizada derivada de la serie hipergeométrica. Fue una de las primeras fracciones continuas analíticas conocidas en… … Wikipedia Español
Teorema de Fuchs — En las matemáticas el teorema de Fuchs, expresa la propiedad de ciertas ecuaciones diferenciales de segundo orden, en cuanto a poseer una solución expresada mediante una serie de potencias. Teorema En las matemáticas, el teorema de Fuch,… … Wikipedia Español
Teorema del número pentagonal — En matemáticas, el teorema del número pentagonal, originalmente formulado por Leonhard Euler, da una equivalencia entre la representación en forma producto y de serie de la función de Euler. Se formula como: Leonhard Euler (1775) … Wikipedia Español
Serie de Leibniz — En matemáticas, la fórmula de Leibniz para el cálculo de π, nombrada así en honor a Gottfried Leibniz, dice que: La expresión de la izquierda es una serie infinita denominada serie de Leibniz, que converge a π ⁄ 4. También se la… … Wikipedia Español
Función generadora — En matemáticas, una función generadora o función generatriz es una serie formal de potencias cuyos coeficientes codifican información sobre una sucesión an cuyo índice corre sobre los enteros no negativos. Hay varios tipos de funciones… … Wikipedia Español

Los diccionarios y las enciclopedias sobre el Académico

Radio de convergencia

Radio de convergencia

Contenido

Definición

Ejemplos

Radio de convergencia finito puys

Distancia a la singularidad

Radio de convergencia infinito

Véase también

Mira otros diccionarios:

Compartir el artículo y extractos

Los diccionarios y las enciclopedias sobre el Académico

Wikipedia Español

Radio de convergencia

Radio de convergencia

Contenido

Definición

Ejemplos

Radio de convergencia finito puys

Distancia a la singularidad

Radio de convergencia infinito

Véase también

Mira otros diccionarios:

Compartir el artículo y extractos

Link directo