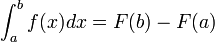- Regla de Barrow
-
Regla de Barrow
En cálculo integral, la regla de Barrow o segundo teorema fundamental del cálculo integral es una propiedad de las funciones continuas y que permite calcular fácilmente el valor de la integral definida a partir de cualquiera de las primitivas de la función.
Recibe su nombre en honor al matemático inglés Isaac Barrow.
Enunciado
Dada una función f(x) contínua en el intervalo [a,b] y sea F(x) cualquier función primitiva de f, es decir F '(x) = f(x). Entonces
Véase también
Categorías: Cálculo integral | Teoremas de cálculo | Integrales
Wikimedia foundation. 2010.