Una función constante es aquella que no depende de ninguna variable y su derivada siempre será cero.

Si f(x) = a , tendremos que f'(x) = 0

Donde a es una constante, como un ejemplo:

f(x) = 7

f'(x) = 0

Contenido 1 Derivada de una constante por una variable 2 Derivada de una potencia entera positiva 3 Derivada de una constante por una función 4 Derivada de una suma 5 Derivada de un producto 6 Derivada de un cociente 7 Véase también

Derivada de una constante por una variable

Cuando una constante acompaña a una variable cuyo exponente es 1 su derivada será el valor de la constante:

f(x) = 7x

Entonces su derivada con respecto a esta variable será:

f'(x) = 7

Derivada de una potencia entera positiva

Una función de carácter exponencial, cuyo exponente es un entero se representa por f(x) = xⁿ y se puede demostrar que su derivada es f'(x) = nx^{n − 1} por ejemplo tomemos la función:

f(x) = x³

Lo primero que se debe hacer es "bajar" el exponente de tal forma que éste multiplique a la variable con respecto a cual estamos derivando, luego al mismo exponente se le resta la unidad formando uno nuevo, así:

f'(x) = 3x^{3 − 1}

Quedando finalmente:

f'(x) = 3x²

En algunas funciones donde la variable ya esta siendo multiplicada, como: f(x) = 7x⁴ se aplica la siguiente regla.

Derivada de una constante por una función

Cuando una función esté representada por medio de f(x) = cxⁿ, su derivada equivale a f'(x) = n(cx^{(n − 1)}) de la siguiente manera:

Consideremos la siguiente función: f(x) = 8x⁴, lo primero a hacer es "bajar" al exponente a multiplicar por la variable y el coeficiente que la acompaña, y de nuevo se halla un nuevo exponente de la misma manera explicada anteriormente:

f'(x) = 4(8x^{4 − 1})

Para obtener

f'(x) = 32x³

Derivada de una suma

Se puede demostrar a partir de la definición de derivada, que la derivada de una suma es la suma de la derivada de cada término por aparte. Es decir, (f + g)' = f' + g'. Como ejemplo consideremos la función f(x) = 3x⁵ + x³, para determinar su derivada se trabaja la derivada de cada termino por aparte y la expresión de estos será la derivada de la función suma:

f'(x) = 15x⁴ + 3x²

Derivada de un producto

La derivada se expresa literalmente de la siguiente forma:

"La derivada de un producto de dos funciones es equivalente a suma entre el producto de la primera función sin derivar y la derivada de la segunda función y el producto de la derivada de la primera función por la segunda función"

Y matemáticamente expresado por la relación 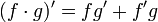. Consideremos la siguiente función como ejemplo:

h(x) = (4x + 2)(3x⁷ + 2)

Identificamos a f(x) = (4x + 2) y g(x) = (3x⁷ + 2), utilizando las reglas anteriormente expuestas, vemos que:

f'(x) = 4 y que g'(x) = 21x⁶

Por lo tanto

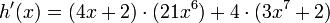
Simplificando y organizando el producto obtenido nos queda

h'(x) = 84x⁷ + 12x⁷ + 42x⁶ + 8

Sumamos términos semejantes y finalmente obtenemos la derivada:

h'(x) = 96x⁷ + 42x⁶ + 8

Derivada de un cociente

La derivada de un cociente se determina por la siguiente relación:

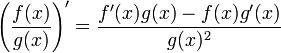
Es decir:

"La derivada de un cociente de dos funciones es la función ubicada en el denominador por la derivada del numerador menos la derivada de la función en el denominador por la función del numerador sin derivar, todo sobre la función del denominador al cuadrado"

Este caso se relaciona mucho con la regla de derivada de un producto, pero hay que tener en cuenta la resta y el orden de los factores. Pero ya explicando lo dicho anteriormente consideremos como ejemplo la siguiente función:

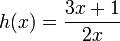
Ahora se trabaja el enunciado anterior el cual nos dice que multipliquemos el denominador que en este caso es g(x) = 2x y se multiplique por la derivada del numerador que seria f'(x) = 3; luego la segunda parte dice que tomemos la función del numerador (f(x)) sin derivar y lo multipliquemos por la derivada de g(x) = 2x, que seria g'(x) = 2, todo esto lo dividimos entre el denominador al cuadrado, asi:

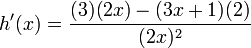
Ahora todo es cuestión de simplificar:

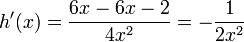
Véase también

• Criterio de la derivada de mayor orden
• Pendiente de una recta
• Límite de una función
• Tabla de derivadas
• Derivación numérica
• Derivación de funciones trigonométricas
• Función matemática
• Integral
• Derivada