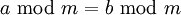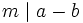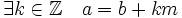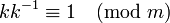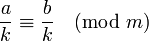Congruencia

Saltar a navegación, búsqueda

Congruencia es un término usado en la teoría de números, para designar que dos números enteros $a$ y $b$ tienen el mismo resto al dividirlos por un número natural $m$ , llamado el módulo; esto se expresa utilizando la notación

$a \equiv b \pmod m$

que se expresa diciendo que $a$ es congruente con $b$ módulo $m$ . Las siguientes expresiones son equivalentes:

$a$ Es congruente con $b$ módulo $m$

$a\equiv b\pmod m$

El resto de $a$ entre $m$ es el resto de $b$ entre $m$

$a\; \bmod \; m = b \; \bmod \; m$

$m$ divide exactamente a la diferencia de $a$ y $b$

$m\mid a-b$

$a$ se puede escribir como la suma de $b$ y un múltiplo de $m$

$\exists k\in \mathbb{Z}\quad a=b+km$

El término congruencia se utiliza además con dos sentidos ligeramente diferentes: por un lado con el sentido de identidad matemática, como ejemplo de este uso tenemos el pequeño teorema de Fermat que asegura que para cada primo $p$ y cada entero $a$ no divisible por $p$ tenemos la congruencia:

$a^{p-1} \equiv 1 \pmod p.$

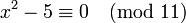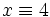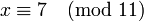Por otro lado se utiliza en el sentido de ecuación, donde aparecen una o más incógnitas, y nos preguntamos si una congruencia tiene solución y en caso afirmativo cuales son todas sus soluciones, por ejemplo la congruencia $x^2 - 5 \equiv 0 \pmod{11}$ , tiene solución, y todas sus soluciones vienen dadas por $x \equiv 4$ y $x\equiv 7 \pmod{11}$ , es decir $x$ puede ser cualquier entero de las sucesiones $11 k + 4$ y $11 k + 7$ . Contrariamente la congruencia 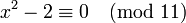$x^2-2 \equiv 0 \pmod{11}$ , no tiene solución.

La notación y la relación terminología fueron introducidas por Carl Friedrich Gauss en su libro Disquisitiones Arithmeticae en 1801. Su utilización se ha extendido a muchos otros entornos en los que podemos hablar de divisibilidad, por ejemplo a polinomios con coeficientes en un cuerpo, a ideales de anillos de números algebraicos, etc.

Propiedades

La relación de congruencia tiene muchas propiedades en común con la igualdad, por citar algunas:

La congruencia para un módulo fijo $m$ es una relación de equivalencia ya que se verifican las propiedades:

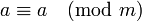
reflexividad: $a \equiv a \pmod m$
simetría: si 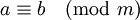$a \equiv b \pmod m$ entonces también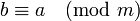 $b \equiv a \pmod m$
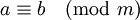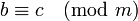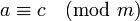transitividad: si $a \equiv b \pmod m$ y $b \equiv c \pmod m$ entonces también $a \equiv c \pmod m$ .

Si $a$ es coprimo con $m$ y 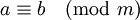$a \equiv b \pmod m$ , entonces $b$ también es coprimo con $m$ .

si 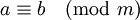$a \equiv b \pmod m$ y $k$ es un entero entonces también se cumple

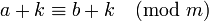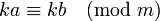
$a+k \equiv b+k \pmod m$ y: $ka \equiv kb \pmod m$

si además $k$ es coprimo con $m$ , entonces podemos encontrar un entero $k - 1$ , tal que

$kk^{-1} \equiv 1 \pmod m$

y entonces tiene perfecto sentido hablar de la división y también es cierto que

$\frac{a}{k} \equiv \frac{b}{k} \pmod m$

donde por definición ponemos $a / k = a k - 1$ .

Como consecuencia de lo anterior, si tenemos dos congruencias con igual módulo:

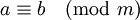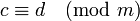
$a\equiv b \pmod m$ y $c \equiv d \pmod m$

podemos sumarlas, restarlas o multiplicarlas de forma que también se verifican las congruencias

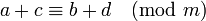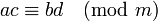
$a+c \equiv b + d \pmod m$ y $ac \equiv bd \pmod m$

Entre Polígonos

Se define la congruencia entre dos polígonos como una correspondencia biunívoca entre sus vértices tal que sus ángulos correspondientes sean congruentes (tengan la misma medida) y los lados correspondientes sean también congruentes (tengan la misma longitud).

Véase también

aritmética modular
resolución de congruencias
clase de congruencia

Obtenido de "Congruencia"

Categorías: Aritmética modular | Relaciones

Wikimedia foundation. 2010.

Игры ⚽ Нужно сделать НИР?

Sinónimos:

coherencia, cohesión, ilación, relación, lógica, pertinencia, conveniencia

Antónimos:

incongruencia

Mira otros diccionarios:

congruencia — sustantivo femenino 1. Relación de coherencia entre dos cosas: Sus actos no guardan congruencia con sus palabras. No existe congruencia entre esa política exterior y los intereses nacionales … Diccionario Salamanca de la Lengua Española
congruência — s. f. 1. Proporção. 2. Relação adequada (entre uma coisa e o fim a que tende). 3. [Teologia católica] Razão do prêmio dado aos merecimentos côngruos … Dicionário da Língua Portuguesa
congruencia — (Del lat. congruentĭa). 1. f. Conveniencia, coherencia, relación lógica. 2. Der. Conformidad entre los pronunciamientos del fallo y las pretensiones de las partes formuladas en el juicio. 3. Mat. Expresión algébrica que manifiesta la igualdad de… … Diccionario de la lengua española
Congruencia — ► sustantivo femenino 1 Relación lógica entre dos acciones o entre elementos de un discurso: ■ no hay congruencia entre el planteamiento y la conclusión. SINÓNIMO coherencia ANTÓNIMO incongruencia 2 DERECHO Relación lógica y de conformidad entre… … Enciclopedia Universal
congruencia — {{＃}}{{LM C09924}}{{〓}} {{SynC10163}} {{［}}congruencia{{］}} ‹con·gruen·cia› {{《}}▍ s.f.{{》}} Coherencia, conformidad, correspondencia o relación lógica. {{＃}}{{LM SynC10163}}{{〓}} {{CLAVE C09924}}{{＼}}{{CLAVE}}{{／}}{{＼}}SINÓNIMOS Y… … Diccionario de uso del español actual con sinónimos y antónimos
Congruencia de triángulos — Saltar a navegación, búsqueda La congruencia de triángulos estudia los casos en que dos o más triángulos presentan ángulos de igual medida o congruentes, así como lados de igual medida o congruentes. Condiciones de congruencia Para que se de la… … Wikipedia Español
Congruencia (geometría) — Un ejemplo de movimiento o congruencia. Las dos figuras de la izquierda son congruentes, mientras que la tercera es semejante a ellas. La última no es ninguna de las dos cosas. Nótese que los movimientos cambian propiedades de las figuras como la … Wikipedia Español
Congruencia (teoría de números) — Para la congruencia vista desde el punto de la geometría elemental, véase congruencia (geometría). Congruencia es un término usado en la teoría de números, para designar que dos números enteros y tienen el mismo resto al dividirlos por un número… … Wikipedia Español
Congruencia de Zeller — La congruencia de Zeller es un algoritmo ideado por Julius Christian Johannes Zeller para calcular el día de la semana de cualquier fecha del calendario. Contenido 1 Fórmula 2 Análisis 3 Algoritmo 3.1 … Wikipedia Español
Congruencia de Mirimanoff — En teoría de números, una congruencia de Mirimanoff es una serie de expresiones en aritmética modular tales que, si se cumplen, conllevan la veracidad del último teorema de Fermat. Ya que el teorema ha sido demostrado, estas expresiones son de… … Wikipedia Español

Los diccionarios y las enciclopedias sobre el Académico

Congruencia

Congruencia

Propiedades

Entre Polígonos

Véase también

Mira otros diccionarios:

Compartir el artículo y extractos

Los diccionarios y las enciclopedias sobre el Académico

Wikipedia Español

Congruencia

Congruencia

Propiedades

Entre Polígonos

Véase también

Mira otros diccionarios:

Compartir el artículo y extractos

Link directo