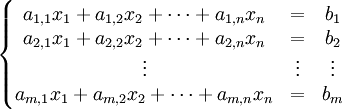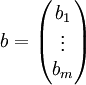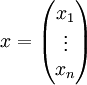Teorema de Rouché-Capelli

Teorema de Rouché-Capelli

Teorema de Rouché-Capelli

Teorema de Rouché-Capelli con algunas variantes también conocido como Teorema de Rouché-Frobenius, se trata de un teorema de álgebra lineal que permite calcular el número de soluciones de un sistema lineal de ecuaciones en función del rango de algunas matrices.

Lleva el nombre del matemático francés Eugène Rouché quien lo ideó y del matemático italiano Alfredo Capelli quien lo enunció de un modo sencillo, o, alternativamente del matemático alemán Ferdinand Georg Frobenius.

Tal teorema establece que para que un sistema de ecuaciones lineales sea compatible es condición necesaria y suficiente que la matriz formada por los coeficientes junto con la ampliada por los términos independientes posean la misma característica. Por lo demás, el sistema constituido estará determinado si su característica coincide con el número de incógnitas ó será indeterminado si posee un valor menor a tal número.

Contenido

El teorema

Un sistema lineal de ecuaciones:

\left\{ \begin{matrix} a_{1,1}x_1 + a_{1,2}x_2 +\cdots + a_{1,n}x_n & = & b_1\\ a_{2,1}x_1 + a_{2,2}x_2 +\cdots + a_{2,n}x_n & = & b_2\\ \vdots & \vdots & \vdots \\ a_{m,1}x_1 +a_{m,2}x_2 + \cdots + a_{m,n}x_n & = & b_m\end{matrix} \right.

Puede ser descrito mediante una matriz:

(A|b) = \left(\begin{matrix} a_{1,1} & \cdots & a_{1,n} \\ \vdots & \ddots & \vdots \\ a_{m,1} & \cdots & a_{m,n} \end{matrix}\right| \left. \begin{matrix} b_1\\ \vdots \\b_m\end{matrix}\right)

dicha matriz asociada al sistema ; está obtenida por la yuxtaposición del la matriz

A = \begin{pmatrix} a_{1,1} & \cdots & a_{1,n} \\ \vdots & \ddots & \vdots \\ a_{m,1} & \cdots & a_{m,n} \end{pmatrix}

de los coeficientes y e una posterior columna

b = \begin{pmatrix} b_1 \\ \vdots \\ b_m \end{pmatrix}

llamada columna de términos notorios. Las matrices A e (A | b) son llamadas respectivamente incompleta (o de los coeficientes) y completa (o ampliada).

Los coeficientes de los sistemas lineares (y por ende de las matrices) son elementos de un campo K , por ejemplo lo es el de los números reales 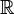\R o complejos \mathbb{C} . Indicándose con rk(M) el rango de una matriz M. El enunciado del teorema de Rouché-Capelli es el siguiente:

Existen soluciones para el sistema si y solo si el rango de la matriz completa es igual al rango de la matriz incompleta.

Entonces, si existen soluciones, éstas forman un subespacio afín de Kn de dimensiones n − rk(A). En particular, si el campo K es infinito tenemos:

  • si rk(A) = n entonces la solución es única,
  • de otro modo existen infinitas posibles soluciones.

Demostración

Existencia

El sistema puede ser descrito de un modo más restringido, introduciendo el vector de las coordenadas

x = \begin{pmatrix} x_1 \\ \vdots \\ x_n \end{pmatrix}

y utilizando el producto entre vectores y matrices, del siguiente modo:

Ax = b

En otros términos, b es la imagen del vector x mediante la aplicación lineal

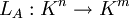
L_A : K^n \to K^ m
LA(x) = Ax

Entonces el sistema admite soluciones si y solo si b es la imagen de cualesquiera vector x de Kn, en otros términos si está en la imagen de LA. Por otro lado, la imagen de LA es generada desde los vectores dados a partir de las columnasA. Entonces b es en la imagen si y solo si el span de las columnas A contiene b, esto es, si y sí el span de las columnas A es igual al span de las columnas de (A | b). Esta última afirmación es equivalente a pedir que las dos matrices posean el mismo rango.

Subespacio afín

Si existe una solución x, toda otra solución se escribe como x + v, donde v es una solución del sistema lineal homogéneo asociado:

Av = 0

En efecto:

A(x + v) = Ax + Av = b + o = b.

Las soluciones del sistema lineal homogéneo asociado son simplemente el núcleo de la aplicación LA. Para el teorema de la dimensión, el núcleo es un subespacio vectorial de dimensión n − rk(A)). Entonces el espacio de las soluciones , obtenido transladando el núcleo con el vector x, es un subespacio afín de la misma dimensión.

Véase también

  • Teorema de la dimensión o teorema del rango
Obtenido de "Teorema de Rouch%C3%A9-Capelli"

Wikimedia foundation. 2010.

Игры ⚽ Поможем сделать НИР

Mira otros diccionarios:

  • Teorema de Rouché–Frobenius — En álgebra lineal, el teorema de Rouché Frobenius permite calcular el número de soluciones de un sistema de ecuaciones lineales en función del rango de la matriz de coeficientes y del rango de la matriz ampliada asociadas al sistema. Lleva el… …   Wikipedia Español

  • Espacio vectorial generado — o span lineal o espacio lineal o lineal hull o capsula lineal. Sea V un espacio vectorial sobre un cuerpo F, y sea S un subconjunto de V. Definimos W como el conjunto generado por S como: Sigue por definición que W es un subespacio vectorial de V …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”