Teorema de la altura

Teorema de la altura

En matemáticas, el teorema de "la altura de un triángulo rectángulo" establece que:

Teorema de la altura (forma 1)

En cualquier triángulo rectángulo la altura relativa a la hipotenusa es la media proporcional entre las proyecciones ortogonales de los catetos sobre la hipotenusa.

Demostración

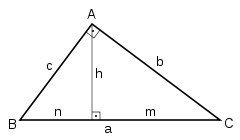
La altura del triángulo rectángulo ABC (véase Figura 1) lo divide en dos triángulos rectángulos semejantes, de forma que

\frac{h}{n} = \frac{m}{h}
Figura 1: Teorema de la altura.

Multiplicando los dos miembros de la igualdad por hn se tiene:

h^2=m\,n \,

por lo que

(1) h=\sqrt{m\,n}

Otra forma del mismo teorema

La altura h correspondiente a la hipotenusa de un triángulo rectángulo (véase Figura 1) también puede obtenerse reemplazando a los valores m y n de la ecuación (1) del presente teorema por sus respectivos equivalentes dados por el teorema del cateto.

m=\frac{b^2}{a} \,    ;    n=\frac{c^2}{a} \,

(h2) h=\sqrt{m\,n}=\sqrt{\frac{b^2}{a}\frac{c^2}{a}}

lo que al simplificar en el último término de la ecuación (h2) la raíz con los cuadrados nos conduce a :

(h3) h=\frac{b\,c}{a}

Donde h es la altura (relativa a la hipotenusa), b y c los catetos y a la hipotenusa.

La ecuación (h3) nos permite establecer el enunciado (forma 2) del teorema :

Teorema de la altura (forma 2)

En todo triángulo rectángulo la altura h (relativa a la hipotenusa) es igual al producto de sus catetos b y c divididos por la hipotenusa a.

Véase también


Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Teorema del cateto — Figura 1 Los segmentos m y n son las respectivas proyecciones de los lados b y a sobre la hipotenusa c, siendo h la altura correspondiente a la hipotenusa. El teorema del cateto establece lo siguiente …   Wikipedia Español

  • Teorema de Euclides (desambiguación) — Diversos teoremas matemáticos deben su nombre al matemático griego Euclides: El lema de Euclides, sobre la divisibilidad por números primos. El teorema de Euclides, sobre la infinitud de los números primos. El teorema de la altura (también… …   Wikipedia Español

  • Teorema del seno — Teorema del seno. En trigonometría, el teorema del seno es una relación de proporcionalidad entre las longitudes de los lados de un triángulo y los senos de los ángulos respectivamente opuestos. Usualmente se presenta de la siguiente forma …   Wikipedia Español

  • Teorema de Pitágoras — El Teorema de Pitágoras establece que en un triángulo rectángulo, el área del cuadrado de la hipotenusa (el lado de mayor longitud del triángulo rectángulo) es igual a la suma de las áreas del cuadrado de los catetos (los dos lados menores del… …   Wikipedia Español

  • Teorema de Tales — Thales de Mileto. Existen dos teoremas en relación a la geometría clásica que reciben el nombre de Teorema de Thales, ambos atribuidos al matemático griego Tales de Mileto en el siglo VI a. C. Contenido 1 …   Wikipedia Español

  • Teorema de equipartición — Figura 1. Movimiento térmico de un péptido tipo hélice α. El movimiento vibratorio es aleatorio y complejo, y la energía de un átomo en particular puede fluctuar ampliamente. Sin embargo, el teorema de equipartición permite que se pueda calcular… …   Wikipedia Español

  • Teorema del coseno — El teorema del coseno es una generalización del teorema de Pitágoras en los triángulos no rectángulos que se utiliza, normalmente, en trigonometría. El teorema relaciona un lado de un triángulo con los otros dos y con el coseno del ángulo formado …   Wikipedia Español

  • Teorema de la bisectriz — En este diagrama, siendo A el ángulo bisecado, BA:AC = BD:DC El teorema de la bisectriz del ángulo interno de un triángulo es un teorema de la geometría elemental la cual es una consecuencia o corolario del Teorema de Tales …   Wikipedia Español

  • Teorema de Viviani — La suma de las longitudes, ℓ + m + n, es igual a la altura del triángulo. El teorema de Viviani, llamado así en honor de Vincenzo Viviani, enuncia que la suma de las distancias desde un punto a cada uno de los lados de un triángulo equilátero es… …   Wikipedia Español

  • Teorema del valor medio — En cálculo diferencial, el teorema de valor medio (de Lagrange), también llamado teorema de los incrementos finitos, teorema de Bonnet Lagrange o teoría del punto medio es una propiedad de las funciones derivables en un intervalo. Algunos… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”