Transformada de Hilbert

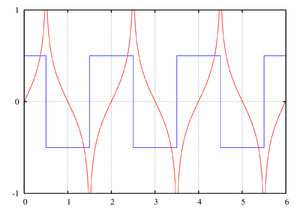Para otros usos de este término, véase Transformación (desambiguación).

La transformada de Hilbert (en rojo) de una onda cuadrada (en azul).

En matemáticas y en procesamiento de señales, la transformada de Hilbert $\mathcal{H}$ , de una función real, $s(t)\,$ , se obtiene mediante la convolución de las señales $s (t)$ y $1 / (π t)$ obteniendo $\widehat s(t)$ . Por lo tanto, la transformada de Hilbert $\widehat s(t)$ se puede interpretar como la salida de un sistema LTI con entrada $s (t)$ y respuesta al impulso $1 / (π t)$ .

Aplicaciones

Es una herramienta matemática útil para describir la envolvente compleja de una señal modulada por una portadora real. Su definición es:

$\widehat s(t) = \mathcal{H}\{s\}(t) = (h*s)(t) = \frac{1}{\pi}\int_{-\infty}^{\infty}\frac{s(\tau)}{t-\tau}\, d\tau.\,$

donde $\scriptstyle h(t) = 1/\pi t$ y considerando la integral como el valor principal (lo que evita la singularidad $\tau = t\,$ ).

Utilizando $\widehat s(t)$ podemos construir la señal analítica de s(t) como:

$s_a(t) = s(t) + i \widehat s(t)$

La transformada de Hilbert posee una respuesta en frecuencia dada por la transformada de Fourier:

$H(\omega ) = \mathcal{F}\{h\}(\omega)\, = \begin{cases}+j\, & \mbox{si } \omega < 0\, \\-j\, & \mbox{si } \omega > 0\,\end{cases}$

o, de manera equivalente:

$H(\omega ) = \mathcal{F}\{h\}(\omega)\, = -j\cdot \sgn(\omega)$

$j\,$ (o también $i\,$ ) es la unidad imaginaria

Y como:

$\mathcal{F}\{\widehat s\}(\omega) = H(\omega )\cdot \mathcal{F}\{s\}(\omega)$ ,

la transformada de Hilbert produce el efecto de desplazar la componente de frecuencias negativas de $s(t)\,$ +90° y las parte de frecuencias positivas −90°.

También tenemos que $H^2(\omega ) = -1\,$ , por lo que multiplicando la ecuación anterior por $-H(\omega )\,$ , obtenemos:

$\mathcal{F}\{s\}(\omega) = -H(\omega )\cdot \mathcal{F}\{\widehat s\}(\omega)$

de donde obtenemos la transformada inversa de Hilbert:

$s(t) = -(h * \widehat s)(t) = -\mathcal{H}\{\widehat s\}(t).\,$

Ejemplos de transformadas

Señal $s(t)\,$	Transformada de Hilbert $\mathcal{H}\{s\}(t)$
$\sin(t)\,$	$-\cos(t)\,$
$\cos(t)\,$	$\sin(t)\,$
$1 \over t^2 + 1$	$t \over t^2 + 1$
$\sin(t) \over t$ Función sinc	$1 - \cos(t) \over t$
$\sqcap(t)$ función rectángulo	${1 \over \pi} \ln \left \| {t+{1 \over 2} \over t-{1 \over 2}} \right \|$
$δ(t)$ Función delta de Dirac	${1 \over \pi t}$

Enlaces externos

Wikiversidad alberga proyectos de aprendizaje sobre Transformada de Hilbert.Wikiversidad

Categorías:

Funciones armónicas
Procesamiento de señales
Transformaciones integrales

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

Transformada integral — Para otros usos de este término, véase Transformada (desambiguación). Una transformada integral es cualquier transformada T aplicada sobre la función f(x) de la forma siguiente: La entrada de esta función T encontramos una función f(t), y la… … Wikipedia Español
David Hilbert — Nacimiento 23 de enero de 1862 Königsberg, Prusia Oriental Fallecimiento 14 de febrero de … Wikipedia Español
Señal analítica — La señal analítica de Gabor correspondiente a una señal temporal real, es una señal compleja cuyo espectro de frecuencias es nulo para frecuencias negativas, y cuya parte real es igual a la señal original. Contenido 1 Definición 2 Construcción… … Wikipedia Español
Transformación — El término transformación hace referencia a la acción o procedimiento mediante el cual algo se modifica, altera o cambia de forma manteniendo su identidad. Adjetivo: transformada, transformado En ciencias sociales Transformación social (redirige… … Wikipedia Español
Transformación (desambiguación) — Saltar a navegación, búsqueda El término transformación, algunas veces expresado como transformada, puede hacer referencia a los siguientes elementos: En matemáticas Transformada de Fourier, Transformada de Fourier discreta y Transformada rápida… … Wikipedia Español
Funciones matemáticas — Anexo:Funciones matemáticas Saltar a navegación, búsqueda Contenido 1 Funciones Elementales 2 Funciones trascendentales 3 Funciones no elementales 4 … Wikipedia Español
Relaciones de Kramers-Kronig — Saltar a navegación, búsqueda En matemáticas y en física, las relaciones de Kramers Kronig describen la relación que existe entre la parte real y la parte imaginaria de ciertas funciones complejas. La condición para que se apliquen a una función… … Wikipedia Español
Anexo:Funciones matemáticas — Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas. Puedes añadirlas así o avisar … Wikipedia Español
Diagrama de Bode — Saltar a navegación, búsqueda Diagrama de Bode de un filtro paso bajo Butterworth de primer orden (con un polo) Un Diagrama de Bode es una representación gráfica que sirve para caracterizar la respuesta en frecuencia de un sistema. Normalmente… … Wikipedia Español
Anexo:Matemáticos importantes — En esta lista de matemáticos importantes se presenta una selección de matemáticos desde la antigüedad hasta el presente. La selección se orienta por los aportes científicos, utilizando como criterio para definir el grado de notoriedad la atención … Wikipedia Español

Los diccionarios y las enciclopedias sobre el Académico

Transformada de Hilbert

Aplicaciones

Ejemplos de transformadas

Enlaces externos

Mira otros diccionarios:

Compartir el artículo y extractos

Los diccionarios y las enciclopedias sobre el Académico

Wikipedia Español

Transformada de Hilbert

Aplicaciones

Ejemplos de transformadas

Enlaces externos

Mira otros diccionarios:

Compartir el artículo y extractos

Link directo