- Funciones matemáticas
-
Anexo:Funciones matemáticas
Contenido
Funciones Elementales
- Funciones polinómicas: Son las funciones P(x), donde P es un polinomio en x, es decir una combinación finita de sumas y productos entre escalares (números) y la variable x. Usualmente, los escalares son números reales, pero en ciertos contextos, los coeficientes pueden ser elementos de un campo o un anillo arbitrario (por ejemplo, fracciones, o números complejos). Ejemplo: 4.5x3 − x.
- Función constante: f(x)= a
- Función lineal: f(x)= ax + b es un binomio del primer grado
- Función cuadrática: F(x)= ax² + bx + c es un trinomio del segundo grado. Ejemplo: 3x2 − 5x + 1
- Función racional: Son funciones obtenidas al dividir una función polinomial por otra, no idénticamente nula.
-
- Ejemplo:
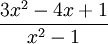
- Ejemplo:
Funciones trascendentales
Cualquier función que no se puede expresar como una solución de una ecuación polinómica se le llama función trascendental.
- Función exponencial
- Función logarítmica
- Funciones trigonométricas: seno, coseno, tangente; secante, cosecante, cotangente; Arcoseno, Arcocoseno, Arcotangente.
- Funciones hiperbólicas: seno hiperbólico, coseno hiperbólico, tangente hiperbólica.
Funciones no elementales
- Función módulo
- Función escalón unitario: En algunos países denominada Heaviside Step.
- Función parte entera
- Función mantisa
- Función signo
- Función de Dirichlet
- Función de Ackermann
- Transformaciones lineales
- Transformada de Hilbert
- Transformada de Laplace
- Transformada de Fourier
- Función hipergeométrica
- Función diferenciable
Funciones de probabilidad
- Distribución de probabilidad
- Densidad de probabilidad
Véase también
Categorías: Anexos:Matemáticas | Funciones reales - Funciones polinómicas: Son las funciones P(x), donde P es un polinomio en x, es decir una combinación finita de sumas y productos entre escalares (números) y la variable x. Usualmente, los escalares son números reales, pero en ciertos contextos, los coeficientes pueden ser elementos de un campo o un anillo arbitrario (por ejemplo, fracciones, o números complejos). Ejemplo: 4.5x3 − x.
Wikimedia foundation. 2010.
