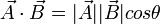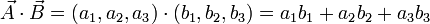Vector (matemática)

Vector (matemática)

Vector (matemática)

Para otros usos de este término, véase vector.

En matemáticas, un vector es un elemento de una estructura algebraica llamada espacio vectorial, que es representada gráficamente con una flecha y esencialmente es un conjunto de elementos con un conjunto de axiomas que debe satisfacer cada uno de ellos. El espacio vectorial más pequeño es el {0} y no hay ninguno que los contenga a todos, ya que cualquier espacio vectorial puede constar de infinitos elementos; por ejemplo, el conjunto de los números reales. Matemáticamente un vector puede ser también un conjunto de elementos ordenados entre sí pero a diferencia de un conjunto normal como el de los números naturales, éste está ordenado.

Así, se llama vector de dimension n a una tupla de n números reales (que se llaman componentes del vector). El conjunto de todos los vectores de dimensión n se representa como 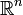\mathbb{R}^n (formado mediante el producto cartesiano).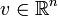

v \in \mathbb{R}^n

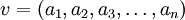
v = (a_1, a_2, a_3, \dots, a_n)

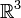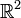Un vector también se puede ver desde el punto de vista de la geometría como vector geométrico (usando frecuentemente el espacio tridimensional \mathbb{R}^3 ó bidimensional \mathbb{R}^2).

Un vector fijo del plano es un segmento orientado, en el que hay que distinguir tres características:

  • dirección: la de la recta que lo contiene
  • sentido: el que va de su origen a su extremo, marcado por una punta de flecha
  • módulo: la longitud del segmento

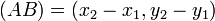
Los vectores fijos del plano se denotan con dos letras mayúsculas, por ejemplo AB, que indican su origen y extremo respectivamente. (AB) = (x_2 - x_1, y_2 - y_1) \,

Contenido

Suma de vectores

La suma ó adición de vectores es una operación interna.

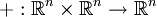
+: \mathbb{R}^n \times \mathbb{R}^n \to \mathbb{R}^n

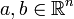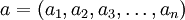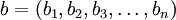Dados dos vectores, a, b \in \mathbb{R}^n. a = (a_1, a_2, a_3, \dots, a_n) y b = (b_1, b_2, b_3, \dots, b_n). Se define la suma como: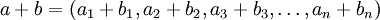

a + b = (a_1 + b_1, a_2 + b_2, a_3 + b_3, \dots, a_n + b_n)

Producto escalar de vectores

El producto escalar de vectores es una operación externa.

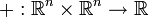
+: \mathbb{R}^n \times \mathbb{R}^n \to \mathbb{R}

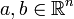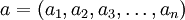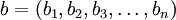Dados dos vectores, a, b \in \mathbb{R}^n. a = (a_1, a_2, a_3, \dots, a_n) y b = (b_1, b_2, b_3, \dots, b_n).

Se representa mediante un punto y se define como:

\vec{A} \cdot \vec{B}=|\vec{A}| |\vec{B}| cos \theta

También lo podemos expresar a partir de sus coordenadas como:

\vec{A}\cdot\vec{B}=(a_1, a_2, a_3)\cdot(b_1,b_2,b_3)=a_1 b_1 + a_2 b_2 + a_3 b_3

Producto de un escalar por un vector

El producto de un escalar por un vector es una operación externa.

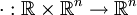
\cdot: \mathbb{R} \times \mathbb{R}^n \to \mathbb{R}^n

El producto de un número escalar cualquiera 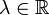\lambda \in \mathbb{R} por un vector 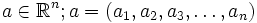a \in \mathbb{R}^n; a = (a_1, a_2, a_3, \dots, a_n) se define como: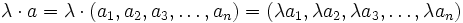

\lambda \cdot a = \lambda \cdot (a_1, a_2, a_3, \dots, a_n) = (\lambda a_1, \lambda a_2, \lambda a_3, \dots, \lambda a_n)

Propiedades fundamentales

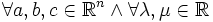
\forall a, b, c \in \mathbb{R}^n \and \forall \lambda, \mu \in \mathbb{R}

  • Propiedad Asociativa: (a + b) + c = a + (b + c)
  • Propiedad Conmutativa: a + b = b + a
  • Elemento opuesto: a + (-a) = 0
  • Elemento neutro: a + 0 = a
  • λ(u + v) = λu + λv
  • (λ + μ)a = aλ + aμ

Véase también: Espacio vectorial.

Notación de un vector

Los vectores se representan mediante dos letras mayúsculas que desmontan el origen y el extremo de un vector, los cuales también superpuesta una flecha, también se puede señalar con una letra minúscula acompañada de una flecha en la parte superior.

  • Ver el portal sobre Vector (matemática) Portal:Matemática Contenido relacionado con Matemática.
Obtenido de "Vector (matem%C3%A1tica)"

Wikimedia foundation. 2010.

Игры ⚽ Поможем сделать НИР

Mira otros diccionarios:

  • vector — VECTÓR, vectori, s.m. Mărime matematică sau fizică definită printr o valoare numerică, o unitate de măsură, o direcţie şi un punct de aplicaţie (reprezentată grafic printr un segment de dreaptă orientat). ♢ (Adjectival) Rază vectoare. – Din fr.… …   Dicționar Român

  • Vector — (Del lat. vector.) ► sustantivo masculino 1 Agente que transporta una cosa de un lugar a otro, en la terminología técnica. 2 MATEMÁTICAS Segmento de recta orientado en el que se distingue un origen y un extremo. 3 MEDICINA Artrópodo que transmite …   Enciclopedia Universal

  • Vector (desambiguación) — El término vector tiene distintos significados de acuerdo al contexto: Contenido 1 En física 2 En matemática 3 En biología 4 En informática y computación …   Wikipedia Español

  • Vector propio y valor propio — Fig. 1. En esta transformación de la Mona Lisa, la imagen se ha deformado de tal forma que su eje vertical no ha cambiado. (nota: se han recortado las esquinas en la imagen de la derecha) …   Wikipedia Español

  • Vector (informática) — Para otros usos de este término, véase Matriz. Matriz unidimensional con 10 elementos. En programación, una matriz o vector (llamados en inglés arrays) es una zona de almacenamiento continuo, que contiene una serie de elementos del mismo tipo,… …   Wikipedia Español

  • Vector de onda — El vector de onda es un vector que apunta en la dirección de propagación de la onda en cuestión y cuya magnitud es el número de onda. Su expresión en matemática es: donde es la dirección de la propagación de la onda. De este modo, para una onda… …   Wikipedia Español

  • Operación matemática — En matemática una operación es la acción de un operador sobre los elementos de un conjunto. El operador toma los elementos iniciales y los relaciona con otro elemento de un conjunto final que puede ser de la misma naturaleza o no; esto se conoce… …   Wikipedia Español

  • Introducción matemática a la relatividad general — La teoría de la relatividad general es una teoría métrica de la gravitación que incorpora además una descripción básica de los sistemas de referencia totalmente generales. Matemáticamente la teoría de la relatividad describe los efectos del campo …   Wikipedia Español

  • Núcleo (matemática) — Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas. Puedes añadirlas así o avisar …   Wikipedia Español

  • Escalar (matemática) — Saltar a navegación, búsqueda Se denomina escalar a los números reales, complejos o racionales que sirven para describir un fenómeno físico con magnitud, pero sin las características vectoriales de dirección o sentido. Formalmente es un tensor de …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”