Escalar (matemática)

Escalar (matemática)

Escalar (matemática)

Se denomina escalar a los números reales, complejos o racionales que sirven para describir un fenómeno físico con magnitud, pero sin las características vectoriales de dirección o sentido. Formalmente es un tensor de rango cero.

En términos matemáticos, se llama escalar a los elementos de un cuerpo (en algunos casos también a los elementos de un anillo), generalmente números, y en particular se usa cuando se quiere distinguirlos claramente de los vectores en el álgebra lineal y en cualquier rama que use módulos o espacios vectoriales.

Contenido

Definición y propiedades

Escalares de espacios vectoriales

Un espacio vectorial se define como un conjunto de vectores, un conjunto de escalares, y una operación de producto escalar que lleva a que un escalar k y un vector v dé un nuevo vector kv. Por ejemplo, en un espacio de coordenadas , el producto escalar k(v1,v2,...,vn) da (kv1,kv2,...,kvn). En una función (lineal) en el espacio, kf es la función x 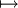\mapsto k(f(x)).

Los escalares se pueden tomar de cualquier campo, incluyendo los números racionales, algebraicos, reales y complejos, así como campos finitos.

Escalares como componentes vectoriales

De acuerdo con el teorema fundamental del álgebra lineal, cada espacio vectorial tiene una base. Se deduce que cada espacio vectorial sobre un campo escalar K es isomorfo a un espacio vectorial de coordenadas, donde las coordenadas son elementos de K. Por ejemplo, cada espacio vectorial real de dimensión n es isomorfo al espacio real de n dimensiones Rn.

Producto escalar

El espacio de producto escalar es un espacio vectorial V con una operación adicional de producto escalar (o producto interno) que permite a dos vectores producir un número. El resultado normalmente está definido como un componente del campo vectorial de V. Como el producto interno de un vector consigo mismo debe ser no-negativo, un espacio de producto escalar solo se puede definir sobre campos que soportan la noción de signo. Lo cuál excluye a los campos finitos, por ejemplo.

La existencia del producto escalar hace posible tener intuición geométrica en un espacio Euclídeo mediante una noción bien definida del ángulo entre dos vectores, y particularmente una manera de expresar cuándo dos vectores son ortogonales. La mayoría de espacios de productos escalares se pueden considerar un espacio vectorial normal de una manera natural.


Véase también

Enlaces externos

Obtenido de "Escalar (matem%C3%A1tica)"

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Escalar — (Del lat. vulgar scalare, escalera.) ► adjetivo 1 FÍSICA Se aplica a la magnitud física y matemática, como la temperatura o la presión, que se expresan sólo con un número. ► verbo transitivo 2 Subir, trepar o ascender por una montaña, pendiente o …   Enciclopedia Universal

  • Vector (matemática) — Saltar a navegación, búsqueda Para otros usos de este término, véase vector. En matemáticas, un vector es un elemento de una estructura algebraica llamada espacio vectorial, que es representada gráficamente con una flecha y esencialmente es un… …   Wikipedia Español

  • Introducción matemática a la relatividad general — La teoría de la relatividad general es una teoría métrica de la gravitación que incorpora además una descripción básica de los sistemas de referencia totalmente generales. Matemáticamente la teoría de la relatividad describe los efectos del campo …   Wikipedia Español

  • Producto escalar — Saltar a navegación, búsqueda En matemáticas el producto escalar, también conocido como producto interno, interior o punto, es una operación definida sobre un espacio vectorial cuyo resultado es una magnitud escalar. Un espacio prehilbertiano es… …   Wikipedia Español

  • Función matemática — En la imagen se muestra una función entre un conjunto de polígonos y un conjunto de números. A cada polígono le corresponde su número de lados. En matemáticas, se dice que una magnitud o cantidad es función de otra si el valor de la primera… …   Wikipedia Español

  • Campo escalar — En matemáticas y física, un campo escalar representa la distribución espacial de una magnitud escalar, asociando un valor a cada punto del espacio. En matemáticas, el valor es un número; en física, una magnitud física. Los campos escalares se… …   Wikipedia Español

  • Operación matemática — En matemática una operación es la acción de un operador sobre los elementos de un conjunto. El operador toma los elementos iniciales y los relaciona con otro elemento de un conjunto final que puede ser de la misma naturaleza o no; esto se conoce… …   Wikipedia Español

  • Matriz (matemática) — Se ha sugerido que Teoría de Matrices sea fusionado en este artículo o sección (discusión). Una vez que hayas realizado la fusión de artículos, pide la fusión de historiales aquí. Para otros usos de este término, véase Matriz. En matemáticas, una …   Wikipedia Español

  • Determinante (matemática) — En matemáticas se define el determinante como una forma multilineal alternada de un cuerpo. Esta definición indica una serie de propiedades matemáticas y generaliza el concepto de determinante haciéndolo aplicable en numerosos campos. Sin embargo …   Wikipedia Español

  • Biología matemática — Saltar a navegación, búsqueda Biología Matemática o Biomatemática es una área interdisciplinaria de estudios que se enfoca en modelamiento de los procesos biológicos utilizando técnicas matemáticas. Tiene grandes aplicaciones teóricas y prácticas …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”