- Velocidad radial
-
La velocidad V(t) de un objeto en la posición x(t) puede descomponerse en una componente radial VR(t), y una transversal VT(t), que dependen de la posición del observador.
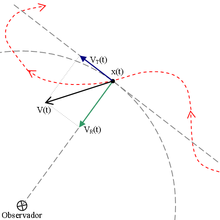
Un planeta suficientemente masivo puede alterar la órbita de su estrella, de manera medible por medio de su velocidad radial.La velocidad radial es la velocidad de un objeto a lo largo de la línea visual del observador. Esto es la componente de la velocidad con la que el objeto se acerca (Corrimiento al azul) o aleja (Corrimiento al rojo) del observador, aunque no se mueva exactamente en dirección de colisión con el observador. Es perpendicular a la velocidad transversal del objeto.
La velocidad radial de una estrella u otros objetos luminosos pero distantes se pueden medir con precisión, tomando una alta resolución del espectro y comparando las medidas de longitud de onda de conocidas líneas espectrales con longitudes de onda a partir de mediciones hechas en un laboratorio. Por convención, una velocidad radial positiva indica que el objeto se aleja, si el signo es negativo, entonces el objeto se acerca.
En muchas estrellas binarias, el movimiento órbital suele causar variaciones de velocidad radial de varios kilómetros por segundo. Como los espectros de estas estrellas pueden variar debido al efecto Doppler, se llaman binarias espectroscópicas. Estudios de velocidad radial pueden ser utilizados para estimar las masas de las estrellas, y algunos elementos orbitales, como la excentricidad y el semieje mayor. El mismo método se ha utilizado también para detectar planetas alrededor de las estrellas, en la forma en que la medición del movimiento determina el periodo orbital del planeta mientras que el tamaño resultante del desplazamiento permite el cálculo del límite inferior de la masa de un planeta. Por ejemplo: La Tierra provoca una variación de velocidad radial de 9 cm/s en nuestro Sol.[1]
Los métodos de velocidad radial sólo pueden revelar un límite inferior, ya que un gran planeta en órbita en un ángulo muy alto para la línea de visión perturbará su estrella radial tanto como un planeta mucho más pequeño con un plano de la órbita en la línea de visión. Se ha sugerido que los planetas con excentricidades altas calculados por este método pueden estar imitando dos sistemas de planetas de órbitas de resonancia circular o casi circular.[2]
Contenido
Velocidad radial tablas comparativas
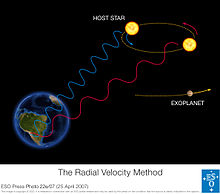El método de velocidad radial para detectar exoplanetas se basa en la detección de las variaciones en la velocidad de la estrella central, debido al cambio de dirección de la fuerza gravitacional de un exoplaneta (no visible) a medida que orbita la estrella. Cuando la estrella se mueve hacia nosotros, su espectro es desplazada al azul mientras que es desplazada hacia el rojo cuando se aleja de nosotros. Regularmente mirando el espectro de una estrella - y así, medir su velocidad - se puede ver si se mueve periódicamente debido a la influencia de un compañero.Masa del
PlanetaDistancia
AUVelocidad radial Júpiter 1 28,4 m/s Júpiter 5 12,7 m/s Neptuno 0,1 4,8 m/s Neptuno 1 1,5 m/s Súper-Tierra (5 M⊕) 0,1 1,4 m/s Súper-Tierra (5 M⊕) 1 0,45 m/s Tierra 1 9 cm/s Ref:[3]
Para las estrellas del tipo MK con planetas en la zona habitable
Masa
Estelar (M☉)Planeta
Masa (M⊕)Lum.
(L0)Tipo RHAB.
(AU)Velocidad
radial
(cm/s)Período
(días)0,10 1,0 8e-4 M8 0,028 168 6 0,21 1,0 7.9e-3 M5 0.089 65 21 0,47 1,0 6.3e-2 M0 0,25 26 67 0,65 1,0 1.6e-1 K5 0,40 18 115 0,78 2,0 4.0e-1 K0 0,63 25 209 Ref:[4]
Oscilación estelar
Oscilación estelar es una variación en la posición de una estrella debido a la influencia gravitacional de otro cuerpo que la orbita. La oscilación estelar es visible como un desplazamiento doppler en el espectro de la estrella o como un movimiento de la estrella en el plano del cielo. El efecto Doppler es causado por que la estrella se mueve hacia y lejos de la Tierra cuando la estrella y su compañero(s) órbitan alrededor de su centro de masa común.
Oscilación estelar es un fenómeno importante en la astronomía, ya que puede ser utilizado para detectar planetas extrasolares y agujeros negros candidatos. En la actualidad, la mayoría de los planetas extrasolares han sido detectados usando el método Doppler, pero varios programas astrométricos se están desarrollando, y que están diseñados para medir el movimiento de la estrella en el plano del cielo.
Efecto Doppler
El Efecto Doppler se produce cuando una fuente de ondas (por ejemplo, luz o sonido) se acerca o aleja del observador. Entonces, la frecuencia de la onda producida por la fuente no es la misma que puede medir el observador. Este es el efecto que ocurre cuando un tren que toca su bocina pasa cerca de nosotros: antes de que pase el sonido se siente más agudo (frecuencia más alta, velocidad radial negativa) que cuando el tren ya se está alejando (frecuencia más baja, velocidad radial positiva).
Uso astronómico
En Astronomía el efecto es aprovechado comúnmente, ya que con el análisis del espectro de la luz que producen los astros, se puede determinar la velocidad radial que tienen con respecto a la Tierra.
Su cálculo se realiza, mediante el análisis de las líneas espectrales producidas por los átomos que componen el objeto observado, utilizando la siguiente fórmula:
donde:
es la velocidad radial medida en kilómetros por hora.
es la velocidad de la luz en kilómetros por hora.
es la longitud de onda de la línea espectral observada, medida en alguna unidad de longitud (como metros o Angstroms). 
es la longitud de onda de la línea espectral en reposo.
Si la velocidad radial es negativa, el objeto se acerca al observador (corrimiento al azul); mientras que si es positiva, el objeto se aleja del observador (corrimiento al rojo).
Si se estima de manera correcta el valor de la masa de la estrella, se puede obtener una medición indirecta de la masa del objeto en órbita. Un buen estimado de la masa puede ser obtenida de su magnitud aparente, la distancia a la que se encuentra y su tipo estelar. El método entrega un límite inferior para la masa del planeta, igual a:
donde:
es el límite inferior para la masa
es la masa real del planeta, e
, es la inclinación del plano orbital del planeta con respecto a la Tierra. Si es posible medir el valor de la inclinación, se puede calcular la masa exacta.
Véase también
- Efecto Doppler
- Espectroscopía Doppler
- Planetas extrasolares
Referencias
- ↑ «ESPRESSO - Searching for other Worlds». Centro de Astrofísica da Universidade do Porto (16-10-2010).
- ↑ Anglada-Escude. «How eccentric orbital solutions can hide planetary systems in 2:1 resonant orbits». The Astrophysical Journal Letters. http://fr.arxiv.org/PS_cache/arxiv/pdf/0809/0809.1275v1.pdf. (web Preprint)
- ↑ «ESPRESSO and CODEX the next generation of RV planet hunters at ESO». Chinese Academy of Sciences (16-10-2010). Consultado el 16-10-2010.
- ↑ «An NIR laser frequency comb for high precision Doppler planet surveys». Chinese Academy of Sciences (16-10-2010). Consultado el 16-10-2010.
Wikimedia foundation. 2010.
