Número de Dedekind

Número de Dedekind
contradicción A y B y C A y B A y C B y C (A y B) o (A y C) (A y B) o (B y C) (A y C) o (B y C) A B C (A o B) y (A o C) y (B o C) <==> (A y B) o (A y C) o (B y C) (A o B) y (A o C) (A o B) y (B o C) (A o C) y (B o C) A o B A o C B o C A o B o C tautología
Los retículos distributivos libres de funciones booleanas monótonas sobre 0, 1, 2 y 3 argumentos.

En combinatoria, los números de Dedekind son una sucesión entera de rápido crecimiento cuyo nombre se dio póstumamente en honor a Richard Dedekind, quien las definió por primera vez en 1897.[1] El número de Dedekind M(n) corresponde, equivalentemente, a lo siguiente:

  • El número de funciones booleanas monótonas de n variables.
  • El número de anticadenas de subconjuntos de un conjunto de n elementos.
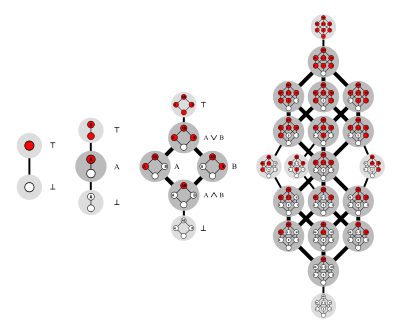
  • El número de elementos en un retículo distributivo libre con n generadores.
  • El número de juegos simples irredundantes definibles sobre n jugadores.
  • El número de hipergrafos minimales completos, definibles sobre un conjunto base de cardinalidad n.
  • El número de familias de Sperner sobre un conjunto de n elementos.

Encontrar una expresión matemática de forma cerrada para M(n) se conoce como el Problema de Dedekind. Aunque existen aproximaciones asintóticas que estiman este número,[2] [3] [4] y una expresión exacta en forma de sumatoria,[5] el cómputo de M(n) sigue siendo ineficiente, y sus valores exactos sólo se conocen para valores n ≤ 8.[6]

Contenido

Ejemplo

Para n = 2, existen seis funciones booleanas monótonas y seis anticadenas de subconjuntos del conjunto de dos elementos {x,y}:

  • La función f(x,y) = falso, que ignora sus valores de entrada y siempre retorna falso, corresponde a la anticadena vacía Ø.
  • La conjunción lógica f(x,y) = x ∧ y corresponde a la anticadena { {x,y} }, que contiene al conjunto {x,y}.
  • La función f(x,y) = x, que ignora su segundo argumento y retorna el primero, corresponde a la anticadena { {x} } que contiene al conjunto {x}.
  • La función f(x,y) = y, que ignora su primer argumento y retorna el segundo, corresponde a la anticadena { {y} } que contiene al conjunto {y}.
  • La disyunción lógica f(x,y) = x ∨ y corresponde a la anticadena { {x}, {y} }, que contiene a los dos conjuntos {x} e {y}.
  • La función f(x,y) = verdadero, que ignora sus valores de entrada y siempre retorna verdadero, corresponde a la anticadena {Ø} que contiene sólo al conjunto vacío.

Valores conocidos

Los valores exactos de los números de Dedekind se conocen para 0 ≤ n ≤ 8. La siguiente tabla muestra tales números, junto con el año y la publicación en que fueron calculados:

Gráfica de los números de Dedekind conocidos, donde se aprecia el crecimiento exponencial de la sucesión.
n Número M(n) Año
0 2 1940[7]
1 3 1940[7]
2 6 1940[7]
3 20 1940[7]
4 168 1940[7]
5 7581 1940[7]
6 7828354 1946[8]
7 2414682040998 1965[9] y 1976[10]
8 56130437228687557907788 1991[6]
(sucesión A000372 en OEIS)

Si n es un número par, entonces M(n) también debería serlo.[11] El cálculo de M(5) = 7581 fue el contraejemplo que desaprobó una conjetura realizada por Garrett Birkhoff que decía que M(n) es siempre divisible por (2n - 1)(2n - 2).[7]

Fórmula con sumatoria

Andrzej Kisielewicz en 1988 demostró la siguiente fórmula para los números de Dedekind:[5]

M(n)=\sum_{k=1}^{2^{2^n}} \prod_{j=1}^{2^n-1} \prod_{i=0}^{j-1} \left(1-b_i^k b_k^k \prod_{m=0}^{\log_2 i} (1-b_m^i+b_m^i b_m^j)\right),

donde

b_i^k=\left\lfloor\frac{k}{2^i}\right\rfloor - 2\left\lfloor\frac{k}{2^{i+1}}\right\rfloor.

Sin embargo, esta fórmula no es útil para el cómputo de los valores de M(n) para n grandes, debido al gran número de términos en la sumatoria.

Asíntotas

El logaritmo de los números de Dedekind puede ser estimado exactamente mediante las cotas

{n\choose \lfloor n/2\rfloor}\le \log_2 M(n)\le {n\choose \lfloor n/2\rfloor}\left(1+O\left(\frac{\log n}{n}\right)\right).

La inecuación de la izquierda cuenta el número de anticadenas en que cada conjunto tiene exactamente \lfloor n/2\rfloor elementos, y la inecuación derecha fue demostrada por Kleitman y Markowsky.[2]

A. D. Korshunov encontró en 1981 una estimación aún mejor:[12]

M(n) = (1+o(1)) 2^{n\choose \lfloor n/2\rfloor}\exp a(n)

para n par, y

M(n) = (1+o(1)) 2^{n\choose \lfloor n/2\rfloor}\exp (b(n)+c(n))

para n impar, donde

a(n)={n\choose n/2-1}(2^{-n/2} + n^2 2^{-n-5} - n2^{-n-4}),
b(n)={n\choose (n-3)/2}(2^{-(n+3)/2} - n^2 2^{-n-6} - n2^{-n+3}),

y

c(n)={n\choose (n-1)/2}(2^{-(n+1)/2} + n^2 2^{-n-4}).

La principal idea detras de estas estimaciones, es que en la mayoría de las anticadenas, todos los conjuntos tienen tamaños muy cercanos a n/2.[13] Para n = 2, 4, 6 y 8, la fórmula de Korshunov provee una estimación imprecisa por un factor de 9.8%, 10.2%, 4.1%, y -3.3%, respectivamente.[14]

Referencias

  1. ↑ Dedekind, Richard (1897), Über Zerlegungen von Zahlen durch ihre größten gemeinsamen Teiler, 2, Gesammelte Werke, pp. 103–148 .
  2. ↑ a b Kleitman, D.; Markowsky, G. (1975), «On Dedekind's problem: the number of isotone Boolean functions. II», Transactions of the American Mathematical Society 213: 373–390, MR0382107 .
  3. ↑ Korshunov, A. D. (1981), «The number of monotone Boolean functions», Problemy Kibernet. 38: 5–108, MR0640855 .
  4. ↑ Kahn, Jeff (2002), «Entropy, independent sets and antichains: a new approach to Dedekind's problem», Proceedings of the American Mathematical Society 130 (2): 371–378, doi:10.1090/S0002-9939-01-06058-0, MR1862115 .
  5. ↑ a b Kisielewicz, Andrzej (1988), «A solution of Dedekind's problem on the number of isotone Boolean functions», Journal für die Reine und Angewandte Mathematik 386: 139–144, doi:10.1515/crll.1988.386.139, MR936995 .
  6. ↑ a b Wiedemann, Doug (1991), «A computation of the eighth Dedekind number», Order 8 (1): 5–6, doi:10.1007/BF00385808, MR1129608 .
  7. ↑ a b c d e f g Church, Randolph (1940), «Numerical analysis of certain free distributive structures», Duke Mathematical Journal 6: 732–734, MR0002842 .
  8. ↑ Ward, Morgan (1946), «Note on the order of free distributive lattices», Bulletin of the American Mathematical Society 52: 423 .
  9. ↑ Church, Randolph (1965), «Enumeration by rank of the free distributive lattice with 7 generators», Notices of the American Mathematical Society 11: 724 . Citado por Wiedemann, 1991.
  10. ↑ Berman, Joel; Köhler, Peter (1976), «Cardinalities of finite distributive lattices», Mitt. Math. Sem. Giessen 121: 103–124, MR0485609 .
  11. ↑ Yamamoto, Koichi (1953), «Note on the order of free distributive lattices», Science Reports of the Kanazawa University 2 (1): 5–6, MR0070608 .
  12. ↑ Korshunov, A. D. (1981), «The number of monotone Boolean functions», Problemy Kibernet. 38: 5–108, MR0640855 .
  13. ↑ Zaguia, Nejib (1993), «Isotone maps: enumeration and structure», en Sauer, N. W.; Woodrow, R. E.; Sands, B., Finite and Infinite Combinatorics in Sets and Logic (Proc. NATO Advanced Study Inst., Banff, Alberta, Canada, May 4, 1991), Kluwer Academic Publishers, pp. 421–430, MR1261220 .
  14. ↑ Brown, K. S., Generating the monotone Boolean functions, http://www.mathpages.com/home/kmath094.htm .

Wikimedia foundation. 2010.

Игры ⚽ Поможем написать реферат

Mira otros diccionarios:

  • Número real — Diferentes clases de números reales. Recta real …   Wikipedia Español

  • Número — Este artículo trata del concepto matemático. Para el concepto lingüístico véase Número gramatical. Para otros usos de este término, véase Número (desambiguación). Un número es una entidad abstracta que representa una cantidad (de una magnitud).… …   Wikipedia Español

  • Número computable — En matemáticas, especialmente en ciencia computacional teórica y lógica matemática, los números computables o recursivos son los números reales que pueden ser computados con la precisión que se desee por un algoritmo finito. Se puede llegar al… …   Wikipedia Español

  • Número de Erdős — El número de Erdős es un modo de describir la distancia colaborativa, en lo relativo a trabajos matemáticos entre un autor y Erdős. El término fue acuñado en honor al matemático húngaro Paul Erdős, uno de los escritores más prolíficos de trabajos …   Wikipedia Español

  • Número natural — Los números naturales pueden usarse para contar (una manzana, dos manzanas, tres manzanas, …). Un número natural es cualquiera de los números que se usan para contar los elementos de un conjunto. Reciben ese nombre porque fueron los primeros que… …   Wikipedia Español

  • Número algebraico — Un número algebraico es cualquier número real o complejo que es solución de una ecuación polinómica de la forma: Donde: , es el grado del polinomio. , los coeficientes del polinomio son números enteros …   Wikipedia Español

  • Número transfinito — En teoría de conjuntos, número transfinito es el término original que el matemático alemán Georg Cantor introdujo para referirse a los ordinales infinitos, esto es, mayor que cualquier número natural o finito, para diferenciarlos del infinito… …   Wikipedia Español

  • Cortaduras de Dedekind — Saltar a navegación, búsqueda Las cortaduras de Dedekind son unos conjuntos de números racionales que representan la primera construcción formal del conjunto de los números reales. Con su aparición se cierra el problema histórico de la… …   Wikipedia Español

  • Función zeta de Dedekind — En matemática, la función zeta de Dedekind es una serie de Dirichlet definida para todo cuerpo K de números algebraicos, expresada como ζK(s) donde s es una variable compleja. Es la suma infinita: realizada sobre todos los I ideales del anillo de …   Wikipedia Español

  • Función eta de Dedekind — No debe confundirse con función zeta de Dedekind o función eta de Dirichlet. Función eta de Dedekind representada en el plano complejo. La función eta de Dedekind o simplemente función η de Dedekind, nombrada así en honor al matemático… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”