Función exponencial

Función exponencial
Funciones exponenciales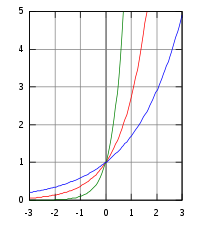
Exponentials.svg
Gráfica de Funciones exponenciales
Definición e^x , \exp(x)\,
Tipo Función real
Dominio (-\infty,+\infty)
Codominio (0,+\infty)
Imagen (0,+\infty)
Propiedades Biyectiva
Convexa
Estrictamente creciente
Trascendente
Cálculo infinitesimal
Derivada e^x \,
Función primitiva e^x \,
Función inversa \ln(x)\,
Límites \lim_{x\to -\infty}\exp(x)= 0\,
\lim_{x\to+\infty}\exp(x)=+\infty\,
Funciones relacionadas Logaritmo

La función exponencial, es conocida formalmente como la función real ex, donde e es el número de Euler, aproximadamente 2.71828.... Esta función tiene por dominio de definición el conjunto de los números reales, y tiene la particularidad de que su derivada es la misma función. Se denota equivalentemente como f(x)=ex o exp(x), donde e es la base de los logaritmos naturales y corresponde a la función inversa del logaritmo natural.

En términos mucho más generales, una función real E(x) se dice que es del tipo exponencial en base a si tiene la forma

E(x)=K \cdot a^x

siendo a, K \in \mathbb{R} números reales, a\geq 0. Así pues, se obtiene un abanico de exponenciales, todas ellas similares, que dependen de la base a que utilicen.

Contenido

Definición formal

La función exponencial ex puede ser definida de diversas maneras equivalentes entre sí, como una serie infinita. En particular puede ser definida como una serie de potencias:

e^x = \sum_{n = 0}^{\infty} {x^n \over n!} = 1 + x + {x^2 \over 2!} + {x^3 \over 3!} + {x^4 \over 4!} + \cdots

o como el límite de la sucesión:

e^x = \lim_{n \to \infty} \left( 1 + {x \over n} \right)^n

Propiedades

La función exponencial (y exponenciales en base distinta a e) satisfacen las siguientes propiedades generales.

  • Son las únicas funciones que son igual a su derivada (multiplicada por una constante, en el caso de que tengan una base distinta a e)
  • \exp(x+y) = \exp(x) \cdot \exp(y)
  • \exp(x-y) = \exp(x) / \exp(y) \,
  • \exp(-x) = {1 \over \exp(x)}
  • \exp(0) = 1 \,
  • su límite en - ∞ es 0, y en + ∞ es + ∞

Derivada

La importancia de las funciones exponenciales en matemática y ciencias radica principalmente de las propiedades de su derivada. En particular,

{d \over dx} e^x = e^x

Es decir, ex es su propia derivada. Es la única función con esa propiedad (sin tomar en cuenta la multiplicación de la función exponencial por una constante). Otras formas de expresar lo anterior:

  • La pendiente del gráfico en cualquier punto es la altura de la función en ese punto.
  • La razón de aumento de la función en x es igual al valor de la función en x.
  • La función es solución de la ecuación diferencial y' = y.

Si la base de la exponencial no es el número e, sino otro número real arbitrario a mayor que 0, entonces la derivada de ésta es:

{d \over dx} a^x = a^x \cdot \ln(a)

donde la función ln denota el logaritmo natural.

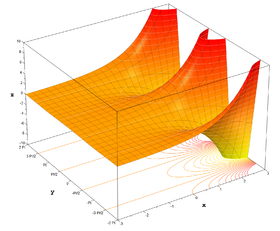
Definición para números complejos

Gráfico de la parte real de una función exponencial en el campo de los complejos
z=\operatorname{Re} \left (\exp \left( x + i y \right)\right)

Como en el caso real, la función exponencial puede ser definida como una función holomorfa en el plano complejo de diferentes maneras. Algunas de ellas son simples extensiones de las fórmulas que se utilizan para definirla en el dominio de los números reales. Específicamente, la forma más usual de definirla para el dominio de los números complejos es mediante la serie de potencias, donde el valor real x se sustituye por la variable compleja z:

e^z = \sum_{n = 0}^{\infty} {z^n \over n!}

para valores imaginarios puros se cumple la identidad

e^{i \cdot t} = \cos t + i \cdot \mbox{sen } t,

en el que un caso particular es la identidad de Euler, conocida también como la fórmula más importante del mundo.

Usando la identidad anterior, donde ahora z=x+yi, con x e y números reales, se obtiene una definición equivalente a la primera,

e^z=e^{x+yi} = e^{x}\cdot(\cos y + i\,\mbox{sen } y)

relación que demuestra que esta función, además de ser holomorfa, es periódica, con un periodo para la parte imaginaria de 2πi.

Véase también

Referencias

  • Abramowitz, M. y Stegun, I. A. . Exponential Function. §4.2 en Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 69-71, 1972.
  • Courant, Richard y Fritz, John. Introducción al cálculo y al análisis matemático Vol.I. Editorial Limusa,1999. ISBN 968-18-0639-5.
  • Apostol, T. M., Calculus. Tomo I. Cálculo con funciones de una variable, con una introducción al Álgebra lineal. Editorial reverte, 2005 ISBN 84-291-5002-1.

Enlaces externos


Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Función exponencial — La función exponencial es la recíproca de la función logaritmo natural. Con esa definición, su dominio es R, pero se puede ampliar al cuerpo de los complejos. Esta función se nota exp: R → R+* donde e es la base de los logaritmos naturales. * * * …   Enciclopedia Universal

  • Exponencial de matrices — Saltar a navegación, búsqueda La exponencial de matrices es una función definida sobre las matrices cuadradas, parecida a la función exponencial. Sea X una matriz nxn de números reales o complejos. La exponencial de X denotada por eX o exp(X) es… …   Wikipedia Español

  • función — (Del lat. functĭo, ōnis). 1. f. Capacidad de actuar propia de los seres vivos y de sus órganos, y de las máquinas o instrumentos. 2. Tarea que corresponde realizar a una institución o entidad, o a sus órganos o personas. 3. Acto solemne,… …   Diccionario de la lengua española

  • exponencial — (De exponente). adj. Dicho del crecimiento: Cuyo ritmo aumenta cada vez más rápidamente. ☛ V. función exponencial …   Diccionario de la lengua española

  • Función trigonométrica compleja — Saltar a navegación, búsqueda Con ayuda de la función exponencial compleja se pueden definir las funciones trigonométricas complejas. Usando la fórmula de Euler: Entonces …   Wikipedia Español

  • Exponencial de una matriz — La exponencial de matrices es una función definida sobre las matrices cuadradas, parecida a la función exponencial. Sea una matriz nxn de números reales o complejos, la exponencial de denotada por o es la matriz dada por la serie de potencia …   Wikipedia Español

  • Función trigonométrica — En matemáticas, Las funciones trigonométricas son las funciones que se definen a fin de extender la definición de las razones trigonométricas a todos los números reales. Las funciones trigonométricas son de gran importancia en física, astronomía …   Wikipedia Español

  • Función — (Del lat. functio, onis.) ► sustantivo femenino 1 BIOLOGÍA Actividad o capacidad de acción específica de un ser vivo y de sus órganos: ■ la función del riñón; la función clorofílica. 2 Desempeño de un cargo u oficio: ■ el vicepresidente desempeña …   Enciclopedia Universal

  • Función W de Lambert — Gráfica de W0(x) para −1/e ≤ x ≤ 4. En matemáticas, la función W de Lambert, denominada así en honor a Johann Heinrich Lambert, si bien también se conoce como función Omega o log producto, es la función inversa de f(w) = wew donde ew es …   Wikipedia Español

  • Función característica — Para otros usos de este término, véase Función indicatriz. La función característica de una variable aleatoria o de su distribución de probabilidad es una función de variable real que toma valores complejos, que permite la aplicación de métodos… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”