- Conexión (matemática)
-
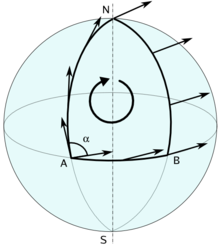 El transporte paralelo de un vector a lo largo de una curva cerrada sobre la esfera, que al igual que el concepto de derivada covariante se basa en la noción de conexión matemática. El ángulo α después de recorrer una vez la curva es proporcional al área dentro de la curva.
El transporte paralelo de un vector a lo largo de una curva cerrada sobre la esfera, que al igual que el concepto de derivada covariante se basa en la noción de conexión matemática. El ángulo α después de recorrer una vez la curva es proporcional al área dentro de la curva.
En geometría diferencial, la conexión es un objeto matemático definido en una variedad diferenciable que permite establecer una relación o "conectar" la geometría local en torno a un punto con la geometría local en torno a otro punto. El caso más sencillo de conexión es una conexión afín que permite especificar una derivada covariante en una variedad diferenciable.
Introducción
La teoría de conexiones conduce a los invariantes de curvatura (véase también tensor de curvatura), y la torsión. Esto se aplica a los fibrados tangentes; hay conexiones más generales, en geometría diferencial: una conexión puede referirse a una conexión en cualquier fibrado vectorial o a una conexión en un fibrado principal.
En un acercamiento particular, una conexión es una 1-forma a valores en un álgebra de Lie que es un múltiplo de la diferencia entre la derivada covariante y la derivada parcial ordinaria. Es decir, la derivada parcial no es una noción intrínseca en una variedad diferenciable: una conexión corrige el concepto y permite la discusión en términos geométricos. Las conexiones dan lugar a un transporte paralelo.
Tipos de conexión
Hay un gran número de enfoques posibles relacionados con el concepto de conexión, entre los cuales están los siguientes:
- Un muy directo estilo módulo a la diferenciación covariante, indicando las condiciones que permiten a los campos vectoriales a actuar sobre secciones de fibrados vectoriales.
- La notación tradicional de índices especifica la conexión por los componentes, vea derivada covariante (tres índices, pero esto no es un tensor).
- En geometría de Riemann hay una manera de derivar una conexión del tensor métrico (conexión de Levi-Civita).
- Usando fibrados principales y formas diferenciales a valores en un álgebra de Lie (véase conexión de Cartan).
- el acercamiento más abstracto puede ser el sugerido por Alexander Grothendieck, donde se considera una conexión como descenso de vecindades infinitesimales de la diagonal.
Las conexiones referidas arriba son conexiones lineales o afines. Hay también un concepto de conexión proyectiva; la forma más comúnmente de esto es derivado de Schwarz en análisis complejo. Vea también: conexión de Gauss-Manin
Véase también
Wikimedia foundation. 2010.
