- Conjetura de Birch y Swinnerton-Dyer
-
La conjetura de Birch y Swinerton-Dyer es una conjetura matemática, enunciada en 1965 por los matemáticos ingleses Bryan Birch y Peter Swinerton-Dyer.
Es uno de los siete problemas del milenio, cuya solución premia el Instituto Clay de Matemáticas con un millón de dólares.
Contenido
Enunciado
La conjetura relaciona los datos aritméticos asociados a una curva elíptica E sobre un cuerpo numérico K con el comportamiento de la Función L de Hasse-Weil L(E, s) de E en s = 1. Concretamente, se conjetura que el rango del grupo abeliano E(Q) de puntos de E es igual al orden del cero de L(E, s) en s = 1, y el primer coeficiente distinto de 0 en la expansión de Taylor de L(E, s) en s = 1 es dado por un mejor refinamiento de datos aritméticos ligados a E sobre Q. En particular, asegura que si L(E, 1) = 0, entonces el grupo E(Q) es infinito, y recíprocamente, si L(E, 1) ≠ 0, entonces E(Q) es finito.[1]
Historia
A principios de la década de1960 Peter Swinnerton-Dyer usó la computadora EDSAC del laboratorio de informática de la universidad de Cambridge para calcular el número de puntos módulo p (denotado por Np) para un número largo de primos p sobre curvas elípticas cuyo rango era conocido. De esos resultados numéricos Bryan Birch y Swinnerton-Dyer conjeturaron que Np para una curva E con rango r obedecía una ley asintótica
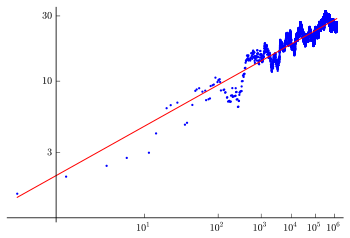Una representación gráfica de
para la curva y2 = x3 − 5x cuando X varia sobre los primeros 100000 primos. El eje X es log(log(X)) y el eje Y está en una escala logarítmica, así, la conjetura predice que los datos podrían formar una línea de pendiente igual al rango de la curva, que es 1 en este caso. Como comparación, una línea de pendiente 1 ha sido dibujada en rojo sobre el gráfico.donde C es una constante.
Inicialmente, se basó en algunas tendencias tenues en algunas gráficas trazadas, lo cual indujo una medida de escepticismo en J. W. S. Cassels (supervisor doctoral de Birch). Pasado el tiempo, las evidencias numéricas se apilaron.
Esto, a su vez, llevó a hacer una conjetura general sobre el comportamiento de la función L de una curva L( E ,s) en s = 1, es decir, que podría tener un cero de orden r en ese punto. Esta conjetura se hizo con visión de futuro en ese momento, dado que la continuación analítica de L( E,s) se estableció sólo para curvas bajo multiplicación compleja, las cuales eran también la principal fuente de ejemplos numéricos. (Nótese que el recíproco de la L-función es desde algunos puntos de vista un objeto más natural de estudio; en ocasiones, esto significa que se podrían considerar los polos en lugar de los ceros)
La conjetura fue ampliada posteriormente para incluir la predicción precisa del coeficiente de Taylor principal de la función L en s = 1. Esto fue conjeturado mediante
donde las cantidades del miembro de la derecha son invariantes de la curva, estudiadas por Cassels, Tate, Shafarevich y otros: éste incluye el orden del grupo de torsión, el orden del grupo de Tate–Shafarevich, y las alturas canónicas de una base de puntos racionales.[1]
Referencias
- ↑ a b Wiles, Andrew (2006), «The Birch and Swinnerton-Dyer conjecture», en Carlson, James; Jaffe, Arthur; Wiles, Andrew (en inglés), The Millennium prize problems, American Mathematical Society, pp. 31–44, ISBN 978-0-821-83679-8, http://www.claymath.org/millennium/Birch_and_Swinnerton-Dyer_Conjecture/birchswin.pdf
Enlaces externos
- Tonterías sobre geometría aritmética (2005, pp. 13-14)
- Descripción oficial del problema (por Andrew Wiles)
- Millennium Prize Problems
Categorías:- Conjeturas matemáticas
- Problemas no resueltos de la matemática
Wikimedia foundation. 2010.
