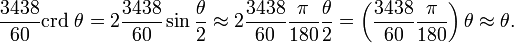Cuerda (geometría)

Cuerda (geometría)

Cuerda (geometría)

Para otros usos de este término, véase Cuerdas.
La línea roja BX es una cuerda.

Una cuerda de una curva es un segmento geométrico, cuyos extremos se encuentran en la curva. La extensión lineal de una cuerda es una secante.

Cuerdas de un círculo

Entre las propiedades de las cuerdas de un círculo se encuentran las siguientes:

  1. Las cuerdas son equidistantes del centro si y solo si sus longitudes son iguales.
  2. Una bisectriz de una cuerda pasa por el centro.
  3. Si las extensiones lineales (líneas secantes) de las cuerdas AB y CD se interceptan en un punto P, entonces sus longitudes satisfacen AP·PB = CP·PD (potencia de un punto).

El área que corta una cuerda circular es denominada un segmento circular.

Cuerdas en trigonometría

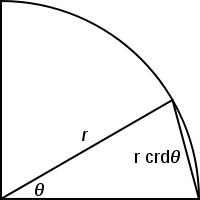
TrigonometricChord.svg

Las cuerdas fueron usadas extensivamente en el desarrollo inicial de la trigonometría. La primera tabla trigonométrica conocida, compilada por Hiparco de Nicea, tabulaba el valor de la función cuerda por cada 7,5 grados.

La función cuerda es definida geométricamente como en la imagen--~ ---- . La cuerda de un ángulo es la longitud dimensional de una cuerda entre dos puntos en una unidad circular separada por un ángulo. Al tomar uno de los puntos como cero, puede fácilmente ser relacionada con la moderna función trigonométrica seno:

\mbox{crd}\ \theta = \sqrt{(1-\cos \theta)^2+\sin^2 \theta} = \sqrt{2-2\cos \theta} = 2 \sqrt{\frac{1-\cos \theta}{2}} = 2 \sin \frac{\theta}{2}.

El último pasa utiliza la fórmula de medio ángulo. Gran parte de la trigonometría moderna se basa en la función seno, mientras que la trigonometría antigua fue construida sobre la base de la función cuerda. Hiparco habría escrito una obra en doce volúmenes sobre las cuerdas. La función cuerda satisface muchas identidades análogas a aquellas modernas bien conocidas:

Nombre Basada en seno Basada en cuerda
Pitagórica sin2θ + cos2θ = 1 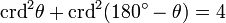\mbox{crd}^2 \theta + \mbox{crd}^2 (180^{\circ} - \theta) = 4
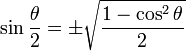
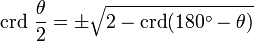
Medio ángulo \sin\frac{\theta}{2} = \pm\sqrt{\frac{1-\cos^2 \theta}{2}} \mbox{crd}\ \frac{\theta}{2} = \pm \sqrt{2-\mbox{crd}(180^{\circ} - \theta)}

La identidad de medio ángulo agiliza enormemente la creación de tablas de cuerdas. Las tablas de cuerdas antiguas solían utilizar un gran valor para el radio del círculo, con lo que era una simple cuestión de escalar para determinar la cuerda necesaria para cualquier círculo. Según G. J. Toomer, Hiparco usó un círculo de radio 3438' (=3438/60=57.3). Este valor es extremadamente cercano al 180 / π (=57.29577951...). Una ventaja de esta elección de radio era que permitía aproximar de forma muy precisa la cuerda de un ángulo pequeño. En términos modernos, permitía una aproximación lineal simple:

\frac{3438}{60} \mbox{crd}\ \theta = 2 \frac{3438}{60} \sin \frac{\theta}{2} \approx 2 \frac{3438}{60} \frac{\pi}{180} \frac{\theta}{2} = \left(\frac{3438}{60} \frac{\pi}{180}\right) \theta \approx \theta.

Enlaces externos

Obtenido de "Cuerda (geometr%C3%ADa)"

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • cuerda — sustantivo femenino 1. Conjunto de hilos de cáñamo, esparto u otro material que retorcidos forman uno solo, grueso y flexible, que sirve generalmente para atar: atar el paquete con cuerdas, tirar de la cuerda, trozo de cuerda. Los secuestradores… …   Diccionario Salamanca de la Lengua Española

  • Cuerda — (Del lat. chorda, cuerda de instrumento.) ► sustantivo femenino 1 Conjunto de hilos o fibras que, retorcidos juntos, forman un cuerpo alargado y flexible que se usa para atar o sujetar cosas: ■ puse todos los libros en cajas y las aseguré con… …   Enciclopedia Universal

  • Geometría — (Del gr. geometria, agrimensura, geometría.) ► sustantivo femenino 1 GEOMETRÍA, MATEMÁTICAS Parte de las matemáticas que estudia el espacio y las figuras y cuerpos que en él se pueden imaginar. FRASEOLOGÍA geometría analítica GEOMETRÍA,… …   Enciclopedia Universal

  • Tangente (geometría) — Este artículo trata sobre el concepto en geometría. Para otros usos de este término, véase tangente (trigonometría). en verde: línea tangente en azul: línea secante en rojo: cuerda Tangente proviene del latín «tangens»=que toca …   Wikipedia Español

  • Arco (geometría) — Saltar a navegación, búsqueda Para otros usos de este término, véase arco. Arco, en geometría, es cualquier curva continua que une dos puntos.[1] También, se denomina arco a un segmento de circunferencia; un arco de circunferencia queda definido… …   Wikipedia Español

  • Cuerdas — Saltar a navegación, búsqueda Cuerdas se puede referir a: El conjunto de instrumentos de cuerda de una orquesta. Una cuerda (física). Una cuerda (geometría). Teoría de cuerdas. Cuerdas vocales. Obtenido de Cuerdas Categoría:… …   Wikipedia Español

  • Toro (matemáticas) — Geometría En geometría, un toro, o toroide, es una superficie de revolución obtenida al desplazar una circunferencia alrededor de un eje coplanar. La esfera es un caso especial de un toro en el que el eje de rotación coincide con un diámetro de… …   Enciclopedia Universal

  • Monocordio — Este artículo forma parte de la categoría: Instrumentos musicales Siglo V aC Pitágoras, define los intervalos musicales experimentando con el monocordio …   Wikipedia Español

  • Ala (aeronáutica) — Ala de un avión en vuelo. Fuerzas sobre el perfil alar …   Wikipedia Español

  • Arco — (Del lat. arcus.) ► sustantivo masculino 1 GEOMETRÍA Porción continua de una línea curva. 2 ARQUITECTURA Construcción curvilínea que cubre un vano en un muro o un espacio entre dos puntos: ■ arco de herradura; arco ojival. 3 MÚSICA Vara delgada,… …   Enciclopedia Universal

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”