- Curva cerrada simple
-
Curva cerrada simple
En topología y en geometría una curva cerrada simple o curva de Jordan es una curva cerrada que no se corta a sí misma.
Contenido
Definición
En general en el mundo de las matemáticas no tan elementales, una función continua (mapeo) e inyectivo;
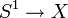 , recibe el nombre de camino cerrado simple en X.
, recibe el nombre de camino cerrado simple en X.Diferenciablemente
En topología y en geometría una curva cerrada simple en un espacio X, es la imagen de una función inyectiva y diferenciable (y con derivada diferente de cero):
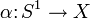 , donde S¹ es la uno-esfera.
, donde S¹ es la uno-esfera.Pero también está la posiblilidad de no disponer diferenciablidad.
Sólo continuidad
Una mapeo
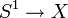 que es continuo e inyectivo, pero no diferenciable, recibe el nombre de trayectoria cerrada en X. Un ejemplo de este tipo gráfico uni-dimensional es el borde de una región triangular, donde tenemos que la orilla describe tres tramos de pendiente constante que tienen intersección dos-a-dos, que son los vértices del triángulo. En estos puntos es donde se pierde la diferenciabilidad.
que es continuo e inyectivo, pero no diferenciable, recibe el nombre de trayectoria cerrada en X. Un ejemplo de este tipo gráfico uni-dimensional es el borde de una región triangular, donde tenemos que la orilla describe tres tramos de pendiente constante que tienen intersección dos-a-dos, que son los vértices del triángulo. En estos puntos es donde se pierde la diferenciabilidad.Se observa que la tipo de trayectoria es diferenciable por trozos.
Véase también
Otros términos utilizados son lazo, nudo o bucle.
Categorías: Topología | Geometría diferencial
Wikimedia foundation. 2010.

