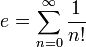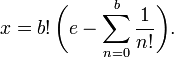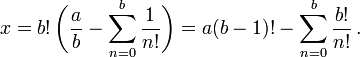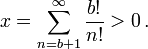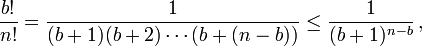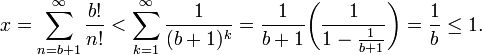Demostración de la irracionalidad de e

Demostración de la irracionalidad de e

Demostración de la irracionalidad de e

Artículo principal: Número e

En matemática, la representación en serie del número e

e = \sum_{n = 0}^{\infty} \frac{1}{n!}

puede ser usado para probar que e es un número irracional. De las tantas representaciones posibles de e, esta es la serie de Taylor para la función exponencial ey evaluada en y = 1.

Demostración

Esta es una prueba por contradicción. Inicialmente e es asumido como un número racional de la forma a/b.
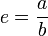
e = \frac{a}{b}

Se define el número

\ x = b!\,\biggl(e - \sum_{n = 0}^{b} \frac{1}{n!}\biggr).

Notar que x es un entero, que substituye e = a/b en esta definición para obtener

x = b!\,\biggl(\frac{a}{b} - \sum_{n = 0}^{b} \frac{1}{n!}\biggr) = a(b - 1)! - \sum_{n = 0}^{b} \frac{b!}{n!}\,.

El primer término es un entero, y cada fracción en la suma es un entero ya que n≤b para cada término. Por lo tanto, x es un entero.

Ahora probaremos que 0 < x < 1. Primero, insertamos la serie representación de e en la definición de x para obtener

x = \sum_{n = b+1}^{\infty} \frac{b!}{n!}>0\,.

Para todos los términos con n ≥ b + 1 tenemos el estimado superior

\frac{b!}{n!} =\frac1{(b+1)(b+2)\cdots(b+(n-b))} \le\frac1{(b+1)^{n-b}}\,,

el cual es estricto aún para cada n ≥ b + 2. Cambiando el índice de la sumatoria a k = n – b y usando la fórmula para la serie geométrica infinita, obtenemos

x =\sum_{n = b+1}^{\infty} \frac{b!}{n!} < \sum_{k=1}^\infty\frac1{(b+1)^k} =\frac{1}{b+1}\biggl(\frac1{1-\frac1{b+1}}\biggr) = \frac{1}{b} \le 1.

Como no hay un entero entre 0 y 1, hemos llegado a una contradicción, y por lo tanto, e debe ser irracional.

Véase también

Obtenido de "Demostraci%C3%B3n de la irracionalidad de e"

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Demostración de la irracionalidad de π — Saltar a navegación, búsqueda Símbolo del número π, popularizado por Leonhard Euler. Aunque la constante matemática conocida como π (pi) ha sido estudiada desde la antigüedad, y también el concepto de número irracional, no fue sin …   Wikipedia Español

  • Raíz cuadrada — Expresión matemática de raíz cuadrada de X . La …   Wikipedia Español

  • Irracional — puede referirse a: Lo opuesto a lo racional. Lo opuesto a la razón (con muchas acepciones: véase razón (desambiguación)). Lo relativo a la irracionalidad (lo opuesto a la racionalidad). Lo relativo al irracionalismo (debe usarse mejor… …   Wikipedia Español

  • Filosofía de la matemática — Saltar a navegación, búsqueda La filosofía de las matemáticas es una rama de la filosofía. Según Michael Dummett puede considerarse que hay cuatro preguntas fundamentales sobre el contenido de la filosofía de las matemáticas: ¿Cómo sabemos que… …   Wikipedia Español

  • Número e — e} es el único número a, tal que la derivada de la función exponencial f(x) = ax (curva azul) en el punto x = 0 es igual a 1. En comparación, las funciones 2x (curva a puntos) y 4x (curva a trazos) son mostradas; no son tangentes a la… …   Wikipedia Español

  • Raíz cuadrada de 2 — La raíz cuadrada de 2 es igual a la longitud de la hipotenusa de un triángulo rectángulo cuyos catetos tienen una longitud 1. La raíz cuadrada de 2, también conocida como constante pitagórica, se denota a menudo como: es un …   Wikipedia Español

  • Exilliteratur — (del alemán: Literatura del Exilio) hace referencia a aquella literatura que es producida por autores que han debido exiliarse, y la cual trata o está influida por este hecho. Normalmente se aplica al exilio de autores alemanes entre 1933 y 1945… …   Wikipedia Español

  • David Hilbert — Nacimiento 23 de enero de 1862 Königsberg, Prusia Oriental Fallecimiento 14 de febrero de …   Wikipedia Español

  • Anexo:Matemáticos importantes — En esta lista de matemáticos importantes se presenta una selección de matemáticos desde la antigüedad hasta el presente. La selección se orienta por los aportes científicos, utilizando como criterio para definir el grado de notoriedad la atención …   Wikipedia Español

  • Caso Dreyfus — Este artículo forma parte de la serie del Caso Dreyfus Artículos de base Cronología · El ejército · Aspectos sociales · El derecho · Hipótesis · Política y diplomacia · La prensa y la edición Documen …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”