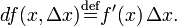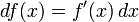- Diferencial de una función
-
Diferencial de una función
- Este artículo habla sobre la definición tradicional del diferencial, para otros usos dentro de la matemática vea diferencial (cálculo, desambiguación), para usos más generales vea diferencial (desambiguación)
En el campo de la matemática llamado cálculo, el diferencial representa un cambio en la linearización de una función. Su definición está basada en la derivada.
Si y representa a una función, entonces el diferencial de dicha función se simboliza dy
Contenido
Definición
El diferencial está definido en los tratamientos modernos del cálculo diferencial de la siguiente manera.[1] El diferencial de una función ƒ(x) de una única variable real x es la función df de dos variables reales e independientes x y Δx dada por:
Uno, o lo dos, argumentos pueden ser suprimidos: ej., se puede ver df(x) o simplemente df. Si y = ƒ(x), el diferencial también puede ser escrito dy. Dado que dx(x, Δx) = Δx es convencional escribir dx = Δx, de manera que la igualdad
se mantiene.
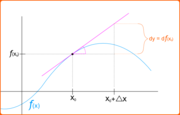
El sentido geométrico del diferencial
El diferencial se puede tomar en el sentido geométrico como la elevación de la tangente desde el punto en que se toma el diferencial.
Recuérdese que la derivada de la función en el punto es la pendiente de la tangente a la función en el punto, al multiplicar esta pendiente por un número obtenemos la elevación de la tangente.
Vista geométricamente, la elevación se produce verticalmente a partir del punto en que se toma el diferencial. El incremento
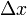 que se tome representará el alejamiento horizontal que haga desde el punto en cuestión.
que se tome representará el alejamiento horizontal que haga desde el punto en cuestión.Así la elevación de la tangente que se obtenga como resultado dependerá del punto en cuestión y del alejamiento horizontal que se tomen, que en la formulas matemáticas están definidos respectivamente por
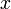 y
y 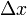 .
.Notas
- ↑ Ver, Courant, 1937i, Kline, 1977, Goursat, 1904, y Hardy, 1905. También Tolstov, 2001 y Ito, 1993, §106.
Referencias
- Stewart, James (2007), Calculus: Early Transcendentals (6th edición), Brooks/Cole, ISBN 978-0495011668
.
- Tolstov, G.P. (2001), "Differential", in Hazewinkel, Michiel, Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1-55608-010-4 .
Categoría: Cálculo
Wikimedia foundation. 2010.