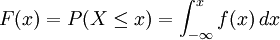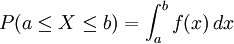Distribuciones continuas

Distribuciones continuas

Distribuciones continuas

Contenido

Conjunto discreto

  • Conjunto discreto. Un conjunto es discreto si está formado por un número finito de elementos, o si sus elementos se pueden enumerar en secuencia de modo que haya un primer elemento, un segundo elemento, un tercer elemento, y así sucesivamente.


Tipos de Variables

  • Variable aleatoria (va). Para un espacio muestral S dado de algún experimento, una variable aleatoria es cualquier regla que asocia un número con cada resultado de S. Las mayúsculas X o Y se utilizan para denotar variables aleatorias. Una va se asocia a la ocurrencia de un fenómeno aleatorio, es el resultado numérico de un experimento aleatorio.
  • Variable aleatoria discreta. Una va es discreta si su conjunto de valores posibles es un conjunto discreto; es decir, toma un número finito de valores numerables.
  • Variable aleatoria continua. Una va continua X es aquella que puede tomar cualquiera de los infinitos valores existentes dentro de un intervalo, tiene un conjunto infinito de valores no numerables; esto es, si para algún a < b, cualquier número x entre a y b es posible.

Al considerar las variables continuas es probable que los datos recabados no sean completamente exactos, o dos o más de ellos no coincidan, por lo que se tiene que trabajar en intervalos.

Distribución de probabilidad para variable continua

Para un variable continua hay infinitos valores posibles de la variable y entre cada dos de ellos se pueden definir infinitos valores más. En estas condiciones no es posible deducir la probabilidad de un valor puntual de la variable; como se puede hacer en el caso de va discretas, pero es posible calcular la probabilidad acumulada hasta un cierto valor (función de distribución de probabilidad), y se puede analizar como cambia la probabilidad acumulada en cada punto (estos cambios no son probabilidades sino otro concepto: la función de densidad.

En el caso de variable continua la distribución de probabilidad es la integral de la función de densidad, por lo que tenemos entonces que:

F(x) = P( X \le x ) = \int_{-\infty}^{x} f(x)\, dx

Sea X una va continua, una distribución de probabilidad o función de densidad de probabilidad (FDP) de X es una función f(x) tal que, para cualesquiera dos números a y b siendo a \le b .


P( a \le X \le b )= \int_{a}^{b} f(x)\, dx


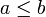La gráfica de f(x) se conoce a veces como curva de densidad, la probabilidad de que X tome un valor en el intervalo [a,b] es el área bajo la curva de la función de densidad; así, la función mide concentración de probabilidad alrededor de los valores de una variable aleatoria continua.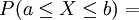


P(a \le X \le b)= área bajo la curva de f(x) entre a y b


Para que f(x) sea una FDP (FDP = f(x)) sea legítima, debe satisfacer las siguientes dos condiciones:


1. f(x) 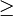\ge \; 0 para toda x.


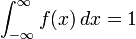
2. \int_{-\infty}^{\infty} f(x)\, dx=1


Ya que la probabilidad es siempre un número positivo, la FDP es una función no decreciente que cumple:


1. 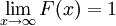\lim_{x \to \infty} F(x) = 1. Es decir, la probabilidad de todo el espacio muestral es 1.


2. 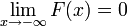\lim_{x \to -\infty} F(x) = 0. Es decir, la probabilidad del suceso nulo es cero.


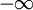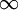Algunas FDP están declaradas en rangos de -\infty \; a \infty \;, como la de la distribución normal.

Distribuciones de variable continua


Enlaces externos.

Commons

Obtenido de "Distribuciones continuas"

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Teoría de distribuciones — En Análisis matemático una distribución, también llamada función generalizada, es un objeto matemático que generaliza la noción de función y la de medida. Además la noción de distribución sirve para extender el concepto de derivada a todas las… …   Wikipedia Español

  • Distribución normal — Saltar a navegación, búsqueda Distribución normal Función de densidad de probabilidad La línea verde corresponde a la distribución normal estandar Función de distribución de probabilidad …   Wikipedia Español

  • Distribución de probabilidad continua — Saltar a navegación, búsqueda En Teoría de la probabilidad una distribución de probabilidad se llama continua si su función de distribución es continua. Puesto que la función de distribución de una variable aleatoria X viene dada por , la… …   Wikipedia Español

  • Matemáticas discretas — Las matemáticas discretas son un área de las matemáticas encargadas del estudio de los conjuntos discretos: finitos o infinitos numerables. En oposición a las matemáticas continuas, que se encarga del estudio de conceptos como la continuidad y el …   Wikipedia Español

  • Distribución uniforme continua — Saltar a navegación, búsqueda Para la distribución discreta, véase Distribución uniforme discreta. Uniforme Función de densidad de probabilidad Utilizando convención de máximo …   Wikipedia Español

  • Distribución normal multivariante — Saltar a navegación, búsqueda Normal multivariante Función de distribución de probabilidad Parámetros (vector real) Σ matriz de covarianza (matriz real definida positiva de dimensión …   Wikipedia Español

  • Función de verosimilitud — En estadística, la función de verosimilitud (o, simplemente, verosimilitud) es una función de los parámetros de un modelo estadístico que permite realizar inferencias acerca de su valor a partir de un conjunto de observaciones. No debe… …   Wikipedia Español

  • Distribución χ² — (ji cuadrado) Función de densidad de probabilidad …   Wikipedia Español

  • Distribución F — Saltar a navegación, búsqueda Fisher Snedecor Función de densidad de probabilidad Función de distribución de probabilidad Parámetros …   Wikipedia Español

  • Distribución de Rayleigh — Saltar a navegación, búsqueda Distribución de probabilidad Rayleigh En la teoría de la probabilidad y estadística, la distribución de Rayleigh es una función de distribución continua. Se suele presentar cuando un vector bidimensional (por ejemplo …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”