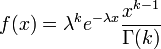Distribución gamma

Distribución gamma

Distribución gamma

Distribución gamma.

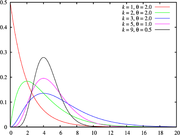
En estadística la distribución gamma es una distribución de probabilidad continua con dos parámetros k y λ cuya función de densidad para valores x > 0 es

f(x) = \lambda^k e^{-\lambda x} \frac{x^{k-1}}{\Gamma(k)}

Aquí e es el número e y Γ es la función gamma. Para valores enteros 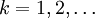k=1,2,\ldots la función gamma queda como Γ(k) = (k − 1)! (siendo ! la función factorial). En este caso —por ejemplo para describir un proceso de Poisson— se llama distribución Erlang con un parámetro θ = 1 / λ.

El valor esperado y la varianza de una variable aleatoria X de distribución gamma son

E[X] = k / λ = kθ
V(X) = k / λ2 = kθ2

Relaciones

El tiempo hasta que el suceso número k ocurre en un Proceso de Poisson de intensidad λ es una variable aleatoria con distribución gamma. Eso es la suma de k variables aleatorias independientes de distribución exponencial con parámetro λ.

Véase también

  • Distribución Beta
  • Distribución Erlang
  • Distribución Ji-cuadrada

Enlaces externos

Obtenido de "Distribuci%C3%B3n gamma"

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Distribución gamma — En estadística la distribución gamma es una distribución de probabilidad continua con dos parámetros y cuya función de densidad para valores es Aquí es el número e y es la …   Enciclopedia Universal

  • Distribución χ² — (ji cuadrado) Función de densidad de probabilidad …   Wikipedia Español

  • Distribución normal — Saltar a navegación, búsqueda Distribución normal Función de densidad de probabilidad La línea verde corresponde a la distribución normal estandar Función de distribución de probabilidad …   Wikipedia Español

  • Distribución de Erlang — Saltar a navegación, búsqueda Distribución de Erlang Función de densidad de probabilidad Función de distribución de probabilidad …   Wikipedia Español

  • Distribución de probabilidad continua — Saltar a navegación, búsqueda En Teoría de la probabilidad una distribución de probabilidad se llama continua si su función de distribución es continua. Puesto que la función de distribución de una variable aleatoria X viene dada por , la… …   Wikipedia Español

  • Distribución exponencial — Saltar a navegación, búsqueda Distribución exponencial Función de densidad de probabilidad Función de distribución de probabilidad …   Wikipedia Español

  • Distribución de la renta — La distribución de la renta es la manera en que se reparten los recursos materiales fruto de la actividad económica en los distintos estratos socio económicos. En general, es independientemente de cómo se obtengan las rentas, su reparto no es… …   Wikipedia Español

  • Distribución de Erlang — En estadística y simulación la distribución (de) Erlang es una distribución de probabilidad continua con dos parámetros y cuya función de densidad para valores es La distribución Erlang es el equivalente de la …   Enciclopedia Universal

  • Distribución de probabilidad — La distribución Normal suele conocerse como la campana de Gauss . En teoría de la probabilidad y estadística, la distribución de probabilidad de una variable aleatoria es una función que asigna a cada suceso definido sobre la variable aleatoria… …   Wikipedia Español

  • Distribución beta — En estadística la distribución beta es una distribución de probabilidad continua con dos parámetros y cuya función de densidad para valores es Aquí es la función gamma. El valor esperado …   Enciclopedia Universal

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”